découverte d'échelles inouïes : 53 + 15 = 68 échelles nonoctaviantes issues de la division du TON égalisé

Exploration des échelles multiples du ton

à la recherche d'échelles nonoctaviantes

le ton, la tonalité, l'intonation
est d'activité millénaire :
le bon ton de l'intonation des tons
occupe énormément d'êtres humains
depuis au moins 3 000 ans avant notre ère
pour entendre la musique refléter nos croyances.
Qui est la musique de l'humanité domestiquée.

LES ECHELLES nonoctaviantes MULTIPLES DU TON ÉGALISÉ

1. avant, dénombrement et identification des échelles octaviantes multiples du ton tonal
de 6 hauteurs ou 200 cents ou 1,12246... = ⁶√2 = 2^1/6= 1,1224620483093729814335330496792

Une division équidistante du ton correspond toujours à un nombre de hauteurs par octave :
Une division équidistante du ton par les nombres entiers (1; 2; 3; etc.) correspond à un nombre de hauteurs paires par octave et génère des intervalles redondants :

nom		description		rapport			quantification en cent
1 ton	<=>	6 hauteurs par octave	<=>	2^1/6	= ⁶√2 = 1,12246	<=>	200
1/2 ton	<=>	12 hauteurs par octave	<=>	2^1/12	= ¹²√2 = 1,05946	<=>	100
1/3 ton	<=>	18 hauteurs par octave	<=>	2^1/18	= ¹⁸√2 = 1,03926	<=>	66,67	download .scl file
1/4 ton	<=>	24 hauteurs par octave	<=>	2^1/24	= ²⁴√2 = 1,0293	<=>	50	download .scl file
1/5 ton	<=>	30 hauteurs par octave	<=>	2^1/30	= ³⁰√2 = 1,02337	<=>	40	download .scl file
1/6 ton	<=>	36 hauteurs par octave	<=>	2^1/36	= ³⁶√2 = 1,01944	<=>	33,34	download .scl file
1/7 ton	<=>	42 hauteurs par octave	<=>	2^1/42	= ⁴²√2 = 1,01664	<=>	28,57	download .scl file
1/8 ton	<=>	48 hauteurs par octave	<=>	2^1/48	= ⁴⁸√2 = 1,01455	<=>	25	download .scl file
1/9 ton	<=>	54 hauteurs par octave	<=>	2^1/54	= ⁵⁴√2 = 1,01292	<=>	22,23	download .scl file
1/10 ton	<=>	60 hauteurs par octave	<=>	2^1/60	= ⁶⁰√2 = 1,01162	<=>	20	download .scl file
1/11 ton	<=>	66 hauteurs par octave	<=>	2^1/66	= ⁶⁶√2 = 1,01056	<=>	18,18	download .scl file
1/12 ton	<=>	72 hauteurs par octave	<=>	2^1/72	= ⁷²√2 = 1,00967	<=>	16,67	download .scl file
1/13 ton	<=>	78 hauteurs par octave	<=>	2^1/78	= ⁷⁸√2 = 1,00893	<=>	15,38	download .scl file
1/14 ton	<=>	84 hauteurs par octave	<=>	2^1/84	= ⁸⁴√2 = 1,00829	<=>	14,28	download .scl file
1/15 ton	<=>	90 hauteurs par octave	<=>	2^1/90	= ⁹⁰√2 = 1,00773	<=>	13,34	download .scl file
1/16 ton	<=>	96 hauteurs par octave	<=>	2^1/96	= ⁹⁶√2 = 1,00725	<=>	12,5	download .scl file
1/17 ton	<=>	102 hauteurs par octave	<=>	2^1/102	= ¹⁰²√2 = 1,00682	<=>	11,7647	download .scl file
...
1/19 ton	<=>	114 hauteurs par octave	<=>	2^1/114	= ¹¹⁴√2 = 1,1,0061	<=>	10,526316

. La division du ton correspond à une progression de 6 en 6 du nombre des degrés divisant l'octave.
. La division de l'octave est toujours paire dans la division du ton même par des nombres premiers.
. Les premières incursions dans la microtonalité ce sont faites à partir de la division du ton (Wyschnégradsky, Carillo, Marie)
. L'écoute peut s'affiner au-delà du 1/16e de ton. Bien que pour Carillo, le 1/16e de ton soit la limite perceptive du plus petit intervalle. Mais la limite perceptive dépend du contexte : de la forme perceptive audible précise, distincte, ambigue, floue ou impossible (Cf. la hauteur un problème d'élévation).

Graphique des 15 premières échelles divisant le ton sur l'ambitus d'une octave :

. On reconnait la forme particulière de l'outil divisionnaire.
. On divise d'abord 16 fois (on peut +) puis on multiplie ensuite à chaque fois par des entiers : ce qui donne un scalage (= striage du temps) 2D (= en 2 dimensions).
Pour favoriser les déambulations scalaires dans une toile (même plusieurs) d'échelles connectées : l'amorce au Champ Scalaire (Scalar Field) pluridimensionnel.

Ce qui nous intéresse : remultiplier ces intervalles par les nombres entiers (1; 2; 3; 4; etc.) afin de trouver des divisions non symétriques pour découvrir d’autres échelles uniques bien qu'elles soient multiples des échelles divisant le ton et, s'extrayant des intervalles-gouffres tels que l'octave, la quinte ou la quarte. Le procédé exploratoire du connu vers l'inconnu.

Graphique des 15 divisions du ton et leurs projections :

Explorons les 8 échelles divisant le ton (de 1/16e de ton à 1/9e de ton) et découvrir leur projections nonoctaviantes.
Les échelles de 1/8e à 1/2 ton sont toutes incluses dans les précédentes.

2. À la recherche des échelles nonoctaviantes tonales (à partir du ton égalisé à 200 cents)

17 est un nombre premier,
ce qui présage d'une récolte
fructueuse d'échelles nonoctaviantes

EXPLORATION DE L'ECHELLE DE 1/17e DE TON
nommable aussi Z102 (à la suite de Pierre Barbaud qui nomma l'échelle chromatique de 12 1/2 tons : Z12) :

0. multiples de 1/17^e de ton

¹⁷√(⁶√2) = ¹⁰²√2 = 2^1/102 = 1,0068187028073552506123281620669 <=> 11,764706 cents

21 échelles multiples :

nom rapport quant. en cent propriété

1 Echelle de 1/17^e de ton (2^1/102)¹ = 1,0068 <=> 11,76 symétrique octaviante = ¹⁰²√2

2 Echelle de 2/17^e de ton (2^1/102)² = 1,01368 <=> 23,53 asymétrique octaviante = ⁵¹√2

3 Echelle de 3/17^e de ton (2^1/102)³ = 1,0206 <=> 35,29 symétrique octaviante = ³⁴√2

4 Echelle de 4/17^e de ton (2^1/96)⁴ = 1,02755 <=> 47,06 asymétrique nonoctaviante

5 Echelle de 5/17^e de ton (2^1/102)⁵ = 1,03456 <=> 58,82 asymétrique nonoctaviante

6 Echelle de 6/17^e de ton (2^1/102)⁶ = 1,0416 <=> 70,58 asymétrique octaviante = ¹⁷√2

7 Echelle de 7/17^e de ton (2^1/102)⁷ = 1,0487 <=> 82,35 asymétrique nonoctaviante

8 Echelle de 8/17^e de ton (2^1/102)⁸ = 1,05587 <=> 94,12 asymétrique nooctaviante

9 Echelle de 9/17^e de ton (2^1/102)⁹ = 1,063 <=> 105,88 asymétrique nonoctaviante

10 Echelle de 10/17^e de ton (2^1/102)¹⁰ = 1,0703 <=> 117,65 asymétrique nonoctaviante

11 Echelle de 11/17^e de ton (2^1/102)¹¹ = 1,0776 <=> 129,41 asymétrique nonoctaviante

12 Echelle de 12/17^e de ton (2^1/102)¹² = 1,08496 <=> 141,17 asymétrique double octaviante = ¹⁷√4

13 Echelle de 13/17^e de ton (2^1/102)¹³ = 1,09236 <=> 152,94 asymétrique nonoctaviante

14 Echelle de 14/17^e de ton (2^1/102)¹⁴ = 1,0998 <=> 164,7 asymétrique nonoctaviante

15 Echelle de 15/17^e de ton (2^1/102)¹⁵ = 1,1073 <=> 176,47 asymétrique nonoctaviante

16 Echelle de 16/17^e de ton (2^1/102)¹⁶ = 1,11486 <=> 188,235 asymétrique nonoctaviante

17 Echelle de ton (2^1/102)¹⁷ = ,12246 <=> 200 symétrique octaviante = ⁶√2 1

18 Echelle de 18/17^e de ton (2^1/102)¹⁸ = 1,13 <=> 211,765 asymétrique nonoctaviante

19 Echelle de 19/17^e de ton (2^1/102)¹⁹ = 1,1378 <=> 223,53 asymétrique triple octaviante = ¹⁷√8

20 Echelle de 20/17^e de ton (2^1/102)²⁰ = 1,14558 <=> 235,3 asymétrique nonoctaviante

21 Echelle de 21/17^e de ton (2^1/102)²¹ = 1,15339 <=> 247,06 asymétrique nonoctaviante

Sur 21 échelles, 5 sont octaviantes et 1 est double octaviante, 1 est triple octaviante et 14 sont nonoctaviantes.

Graphe des 19 premières échelles multiples de 1/17^e de ton :

. Le cycle de chacune de ces échelles se répète tous les 17 degrés. Elles sont donc toutes asymétriques.
. Toutes ses échelles sont cycliques de ton en ton : de 1 à 19 tons sur le graphe
. 19/17e de ton trouve son cycle à 3800 cents = 3 8ves + 3ce M
. Les intervalles des cycles sont tous de Z12.

Les 14 échelles nonoctaviantes + 1 triple octaviante tirées de 1/17e de ton :

nom rapport en cent

1 Echelle de 4/17^e de ton 1,02755 47,06

2 Echelle de 5/17^e de ton 1,03456 58,82

3 Echelle de 7/17^e de ton 1,0487 82,35

4 Echelle de 8/17^e de ton 1,05587 94,12

5 Echelle de 9/17^e de ton 1,063 105,88

6 Echelle de 10/17^e de ton 1,0703 117,65

7 Echelle de 11/17^e de ton 1,0776 129,41

8 Echelle de 13/17^e de ton 1,09236 152,94

9 Echelle de 14/17^e de ton 1,0998 164,7

10 Echelle de 15/17^e de ton 1,1073 176,47

11 Echelle de 16/17^e de ton 1,11486 188,235

12 Echelle de 18/17^e de ton 1,13 211,765

13 Echelle de 19/17^e de ton 1,1378 223,53

14 Echelle de 20/17^e de ton 1,14558 235,3

15 Echelle de 21/17^e de ton 1,15339 247,06

1. L'échelle 4/17^e de ton à 47,06 cents divise l'intervalle de sixte mineure (800 cents) en 17 intervalles équidistants

...

2. L'échelle 5/17^e de ton à 58,82 cents divise l'intervalle de septième mineure (1000 cents) en 17 intervalles équidistants

00° : unisson
01° : 58.82 cents
02° : 117.65 cents
03° : 176.47 cents
04° : 235.29 cents
05° : 294.12 cents
06° : 352.94 cents
07° : 411.765 cents
08° : 470.59 cents
09° : 529.41 cents
10° : 588.235 cents
11° : 647.059 cents
12° : 705.882 cents
13° : 764.706 cents
14° : 823.529 cents
15° : 882.353 cents
16° : 941.176 cents
17° : 1000 cents

...

3. L'échelle 7/17^e de ton à 82,35 cents divise l'intervalle d'8ve + 2de M (1400 cents) en 17 intervalles équidistants

...

4. L'échelle 8/17^e de ton à 94,12 cents divise l'intervalle d'8ve + 3ce M (1600 cents) en 17 intervalles équidistants

...

5. L'échelle 9/17^e de ton à 105,88 cents divise l'intervalle d'8ve + 4te+ (1800 cents) en 17 intervalles équidistants

...

6. L'échelle 10/17^e de ton à 117,65 cents divise l'intervalle d'8ve + 6te m (2000 cents) en 17 intervalles équidistants

...

7. L'échelle 11/17^e de ton à 129,41 cents divise l'intervalle d'8ve + 7e m (2200 cents) en 17 intervalles équidistants

...

8. L'échelle 13/17^e de ton à 152,94 cents divise l'intervalle de double 8ve + 2de M (2600 cents) en 17 intervalles équidistants

...

9. L'échelle 14/17^e de ton à 164,7 cents divise l'intervalle de double 8ve + 3ce M (2800 cents) en 17 intervalles équidistants

...

10. L'échelle 15/17^e de ton à 176,47 cents divise l'intervalle de double 8ve + 4te+ (3000 cents) en 17 intervalles équidistants

...

11. L'échelle 16/17^e de ton à 188,235 cents divise l'intervalle de double 8ve + 6te m (3200 cents) en 17 intervalles équidistants

...

12. L'échelle 18/17^e de ton à 211,765 cents divise l'intervalle de double 8ve + 7e m (3400 cents) en 17 intervalles équidistants

...

13. L'échelle 19/17^e de ton à 223,53 cents divise l'intervalle de triple 8ve (3600 cents) en 17 intervalles équidistants

...

14. L'échelle 20/17^e de ton à 235,3 cents divise l'intervalle de triple 8ve + 2de M (3800 cents) en 17 intervalles équidistants

...

15. L'échelle 21/17^e de ton à 247,06 cents divise l'intervalle de triple 8ve + 3ce M (4000 cents) en 17 intervalles équidistants

...

Pourquoi RE « Commencer avec l'échelle de 1/16e de ton » ?
Nous savons a priori que la formation des échelles nonoctaviantes ne dépend pas du PPID = du plus petit intervalle distinguable,
mais de la 1ère échelle nonoctaviante extraite qui elle dépend du PPID = du plus petit intervalle distinguable.

EXPLORATION DE L'ECHELLE DE 1/16e DE TON
nommable aussi Z96 (à la suite de Pierre Barbaud qui nomma l'échelle chromatique de 12 1/2 tons Z12) :

1. multiples de 1/16^e de ton

¹⁶√(⁶√2) = ⁹⁶√2 = 2^1/96 = 1,0072464122237038980903435690978...

16 échelles multiples jusqu'au ton :

nom rapport quant. en cent propriété

1 Echelle de 1/16^e de ton (2^1/96)¹ = 1,00725 <=> 12,5 cents symétrique octaviante = ⁹⁶√2

2 Echelle de 1/8^e de ton (2^1/96)² = 1,0145526 <=> 25 cents symétrique octaviante = ⁴⁸√2

3 Echelle de 3/16^e de ton (2^1/96)³ = 1,02191 <=> 37,5 cents symétrique octaviante = ³²√2 download .scl file

4 Echelle de 1/4 de ton (2^1/96)⁴ = 1,02932 <=> 50 cents symétrique octaviante = ²⁴√2

5 Echelle de 5/16^e de ton (2^1/96)⁵ = 1,03678 <=> 65,5 cents symétrique nonoctaviante

6 Echelle de 3/8^e de ton (2^1/96)⁶ = 1,0443 <=> 75 cents symétrique octaviante = ¹⁶√2 download .scl file

7 Echelle de 7/16^e de ton (2^1/96)⁷ = 1,05187 <=> 87,5 cents symétrique nonoctaviante

8 Echelle de 1/2 de ton (2^1/96)⁸ = 1,05946 <=> 100 cents symétrique octaviante = ¹²√2

9 Echelle de 9/16^e de ton (2^1/96)⁹ = 1,06717 <=> 112,5 cents symétrique nonoctaviante

10 Echelle de 5/8^e de ton (2^1/96)¹⁰ = 1,07491 <=> 125 cents symétrique nonoctaviante

11 Echelle de 11/16^e de ton (2^1/96)¹¹ = 1,08448 <=> 137,5 cents symétrique nonoctaviante

12 Echelle de 3/4 de ton (2^1/96)¹² = 1,09055 <=> 150 cents symétrique octaviante = ⁸√2 download .scl file

13 Echelle de 13/16^e de ton (2^1/96)¹³ = 1,09846 <=> 162,5 cents symétrique nonoctaviante

14 Echelle de 7/8^e de ton (2^1/96)¹⁴ = 1,10642 <=> 175 cents symétrique nonoctaviante

15 Echelle de 15/16^e de ton (2^1/96)¹⁵ = 1,11445 <=> 187,5 cents symétrique nonoctaviante

16 Echelle de ton (2^1/96)¹⁶ = 1,12253 <=> 200 cents symétrique octaviante = ⁶√2

. remarque 1 :

L'échelle de ton <=> 2^1/6= 1,12246 contre 1,12253 pour (2^1/96)¹⁶montre la relativité de l’exactitude des chiffres.
pour l’échelle de ton mieux connue sous le nom de "gamme par ton" et attachée à Debussy. Échelle à la sonorité si particulière.

. remarque 2 :

Il n'y a pas d'échelle asymétrique nonoctaviante et pas d'échelle asymétrique octaviante dans les 16 projections multiples des 16 échelles multiples de 1/16e de ton (de Z96).

Graphe des 16+1 premières échelles multiples de 1/16^e de ton :

. Le cycle de chaque échelle se répète tout les 8 degrés.
. Toutes les échelles multiples de 1/16e de ton répètent un cycle d'un intervalle inclus dans Z12.
. Dans cette famille, l'échelle chromatique (Z12) et par ton (Z6) répètent un cycle de 8 degrés et non de 12 et 6.
. Ces échelles octotoniques, répétant un cycle de 8 degrés reconnaissent un centre de symétrie dans leurs divisions et sont donc toutes symétriques.
. Des 16 échelles multiplent de Z96 (de 1/16e de ton à 16/16e de ton) 8 sont octaviantes et 8 sont nonoctaviantes : égalité !

Nous avons 8 échelles premières nonoctaviantes multiples de l’échelle d’1/16e de ton :

telles que les échelles de :

nom quantification en cent rapport

5/16^e de ton 62,5 cents (⁹⁶√2)⁵ = 1,03678...

7/16^e de ton 87,5 cents (⁹⁶√2)⁷ = 1,05187...

9/16^e de ton 112,5 cents (⁹⁶√2)⁹ = 1,06717...

5/8^e de ton 125 cents (⁹⁶√2)¹⁰ = 1,07491...

11/16^e de ton 137,5 cents (⁹⁶√2)¹¹ = 1,0827...

13/16^e de ton 162,5 cents (⁹⁶√2)¹³ = 1,09846...

7/8^e de ton 175 cents (⁹⁶√2)¹⁴ = 1,10642...

15/16^e de ton 187,5 cents (⁹⁶√2)¹⁵ = 1,11445...

17/16^e de ton 212,5 cents (⁹⁶√2)¹⁷ = 1,13066...

9/8^e de ton 225 cents (⁹⁶√2)¹⁸ = 1,13886...

19/16^e de ton 237,5 cents (⁹⁶√2)¹⁹ = 1,14712...

11 échelles cycliques symétriques nonoctaviantes multiples de l’échelle 1/16e de ton (12,5 cents) ⁹⁶√2=1,00725.

Graphe des 8 premières échelles cycliques symétriques nonoctaviantes multiples de l'échelle de 1/16^e de ton :

Même si la symétrie de l'octave par l'existence du triton (4te+) n'apparait pas, ces échelles divisent un cycle par un nombre pair et donc reconnaissent un centre de symétrie dans leurs divisions. Elles sont symétriques, car elles possèdent un degré central (le pli du miroir) où la demi-échelle miroir correspond à la demi-échelle projetée.

Propriétés de ces 8 échelles nonoctaviantes multiples de 1/16e de ton (12,5 cents ou ⁹⁶√2=1,00725) :

1. L'échelle 5/16e de ton (62.5 cents) divise l'intervalle de quarte (500 cents) en 8 intervalles équidistants et reproduit les intervalles de septième mineur (2 . 4te) et octave+3ce mineure (3 . 4te), etc. : 5/16e de ton est une échelle cyclique qui répète l'intervalle de 4te et ses multiples. Reste la prégnance de l'octave au 19e degré, même si celui-ci est plus petit (1187,5 cents).
0° : unisson
1° : 62,5 cents
2° : 125 cents
3° : 187,5 cents
4° : 250 cents             2M+1/4 de ton
5° : 312,5 cents
6° : 375 cents
7° : 437,5 cents
8° : 500 cents            4te
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

2. L'échelle 7/16e de ton (87.5 cents) divise l'intervalle de quinte (700 cents) en 8 intervalles équidistants et reproduit les intervalles d'octave+2de majeur (2 . 5te), etc. : 7/16e de ton est une échelle cyclique qui répète l'intervalle de 5te et ses multiples. Reste la prégnance de l'octave au 14e degré, même si celui-ci est plus grand (1225 cents).
0° : unisson
1° : 87,5 cents
2° : 175 cents
3° : 262,5 cents
4° : 350 cents           3m+1/4 de ton
5° : 437,5 cents
6° : 525 cents
7° : 612,5 cents
8° : 700 cents            5te
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

3. L'échelle 9/16e de ton (112.5 cents) divise l'intervalle de sixte majeure (900 cents) en 8 intervalles équidistants et reproduit les intervalles d'octave+4te+ (2 . 6teM), etc. : 9/16e de ton est une échelle cyclique qui répète l'intervalle de 6teM et ses multiples. Reste la prégnance de l'octave au 11e degré, même si celui-ci est plus grand avec battement (1237,5 cents).
00° : unisson
01° : 112,5 cents
02° : 225 cents
03° : 337,5 cents
04° : 450 cents          3M+1/4 de ton
05° : 562,5 cents
06° : 675 cents
07° : 787,5 cents
08° : 900 cents          6M

09° : 1012,5 cents
10° : 1125 cents
11° : 1237,5 cents
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

4. L'échelle 5/8e de ton (125 cents) est inclus (et multiple par 2) dans l'échelle 5/16e de ton. 5/8e de ton divise l'intervalle de quarte (500 cents) en 4 intervalles équidistants et reproduit les intervalles de septième mineur 2 . 4te (1000 cents) et octave+3ce mineure 3 . 4te (1500 cents), etc. : 5/8e de ton est une échelle cyclique qui répète l'intervalle de 4te et ses multiples. Reste la prégnance de l'octave au 10e degré, même si celui-ci est plus grand (1250 cents contre 1200) d'1/4 de ton.
00° : unisson
01° : 125 cents
02° : 250 cents         2M+1/4 de ton
03° : 375 cents
04° : 500 cents         4te

05° : 625 cents
06° : 750 cents         5te+1/4 de ton
07° : 875 cents
08° : 1000 cents        7m
09° : 1125 cents
10° : 1250 cents        8ve+1/4 de ton
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

5. L'échelle 11/16e de ton (137.5 cents) divise l'intervalle de septième majeur (1100 cents) en 8 intervalles équidistants et reproduit les intervalles d'octave+septième mineur (2 . 7eM), etc. : 11/16e de ton est une échelle cyclique qui répète l'intervalle de 7eM et ses multiples. Reste la prégnance de l'octave au 9e degré, même si celui-ci est plus grand avec battement (1237,5 cents).
0° : unisson
1° : 137,5 cents
2° : 275 cents
3° : 412,5 cents
4° : 550 cents          4te + 1/4 de ton
5° : 687,5 cents
6° : 825 cents
7° : 962,5 cents
8° : 1100 cents        7M

9° : 1237,5 cents [proche 8ve : à 37,5 cents]
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

6. L'échelle 13/16e de ton (162.5 cents) divise l'intervalle d'octave et seconde mineure (1300 cents) en 8 intervalles équidistants et reproduit les intervalles de deux octaves+seconde majeur, etc. : 13/16e de ton est une échelle cyclique qui répète l'intervalle de 8ve+2dem et ses multiples. Aucune prégnance d'intervalles connus trop importante.
0° : unisson
1° : 162,5 cents
2° : 325 cents
3° : 487,5 cents
4° : 650 cents         4+ & 1/4 de ton
5° : 812,5 cents
6° : 975 cents
7° : 1137,5 cents
8° : 1300 cents        8ve+2m
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

7. L'échelle 7/8e de ton (175 cents) est inclus (et multiple de 2) dans l'échelle 7/16e de ton. 7/8e de ton divise l'intervalle de quinte (700 cents) en 4 intervalles équidistants et reproduit les intervalles d'octave+2de majeur (2 . 5te), etc. : 7/8e de ton est une échelle cyclique qui répète l'intervalle de 5te et ses multiples. Reste la prégnance de l'octave au 7e degré, même si celui-ci est plus grand (1225 cents) d'1/8e de ton.
0° : unisson
1° : 175 cents
2° : 350 cents           3m+1/4 de ton
3° : 525 cents
4° : 700 cents           5te

5° : 875 cents
6° : 1050 cents         7m+1/4 de ton
7° : 1225 cents         [proche 8ve : à 25 cents]
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

8. L'échelle 15/16e de ton (187.5 cents) divise l'intervalle d'octave et tierce mineur (1500 cents) en 8 intervalles équidistants. Aucune prégnance d'intervalles connus trop importante.
0° : unisson
1° : 187,5 cents
2° : 375 cents
3° : 562,5 cents
4° : 750 cents           5te+1/4 de ton
5° : 937,5 cents
6° : 1125 cents
7° : 1312,5 cents
8° : 1500 cents          8ve+3m
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

9. L'échelle de 17/16e de ton (212,5 cents) divise l'intervalle doctave et quarte (1700 cents) en 8 intervalles équidistants. Prégnance au 9e degré proche de l'intervalle 8ve+5te.
0° : unisson
1° : 212,5 cents
2° : 425 cents
3° : 637,5 cents
4° : 850 cents          6m+1/4 de ton
5° : 1062,5 cents
6° : 1275 cents
7° : 1487,5 cents
8° : 1700 cents         8ve+4te

9° : 1912,5 cents      [proche 8ve+5te : à 12,5 cents]

10. L'échelle de 9/8e de ton (225 cents) divise l'intervalle de sixte majeur (900 cents) en 4 intervalles équidistants. Prégnance unique au 7e degré avec 8ve+3ceM bien qu'il y ait une différence d'1/8e de ton.
0° : unisson
1° : 225 cents
2° : 450 cents      3M+1/4 de ton
3° : 675 cents
4° : 900 cents      6M

5° : 1125 cents     8ve -3/8e de ton
6° : 1350 cents     8ve+3/4 de ton
7° : 1575 cents     [proche 8ve+3ceM : à 25 cents]

11. L'échelle de 19/16e de ton (237,5 cents) divise l'intervalle d'8ve+5te (1900 cents) en 8 intervalles équidistants. Prégance de l'octave au 5e degré bien qu'il y ait une différence d'1/16e de ton.
0° : unisson
1° : 237,5 cents
2° : 475 cents
3° : 712,5 cents
4° : 950 cents
5° : 1187,5 cents    [proche 8ve : à 12,5 cents]
6° : 1425 cents
7° : 1662,5 cents
8° : 1900 cents       8ve+5te

Récapitulation :

rang nom en ton ambitus tonal (intervalle) divisé divisant par nonoctaviation intervalle en cents nombre de degrés par 8ve désignation par densité

1 5/16^e de ton 500 cents 4te 8 au 19e degré : 1187,5 contre 1200 cents 62,5 19,2 nanodécatonique nonoctaviante

2 7/16^e de ton 700 cents 5te 8 au 14e degré : 1225 contre 1200 cents 87,5 13,714... tetradécatonique nonoctaviante

3 9/16^e de ton 900 cents 6te M 8 au 11e degré : 1237,5 contre 1200 cents 112 10,714... hendécatonique nonoctaviante

4 5/8^e de ton 500 cents 4te 4 au 10e degré : 1250 contre 1200 cents 125 9,6 décatonique nonoctaviante

5 11/16^e de ton 1100 cents 7e M 8 au 9e degré : 1237,5 contre 1200 cents 137,5 8,72.. nonatonique nonoctaviante

6 13/16^e de ton 1300 cents 8ve+2de m 8 au 7e degré : 1137,5 contre 1200 cents 162,5 7,384... heptatonique nonoctaviante

7 7/8^e de ton 700 cents 5te 4 au 7e degré : 1225 contre 1200 cents 175 6,857... heptatonique nonoctaviante

8 15/16^e de ton 1500 cents 8ve+3ce m 8 au 6e degré : 1125 contre 1200 cents 187,5 6,4 hexatonique nonoctaviante

9 17/16^e de ton 1700 cents 8ve+4te 8 au 5e degré : 1275 contre 1200 cents 212,5 5,647... hexatonique nonoctaviante

10 9/8^e de ton 900 cents 6te M 4 au 4e degré : 1125 contre 1200 cents 225 5,33.. pentatonique nonoctaviante

11 19/16^e de ton 1900 cents 8ve+5te 8 au 5e degré : 1187,5 contre 1200 cents 237,5 5,0526... pentatonique nonoctaviante

Remarques :

. Les 8 premières échelles nonoctaviantes de l'ensemble Z96 (1/16e de ton) sont toutes cycliques et divisent le cycle en nombre d'intervalles pairs par 8 ou 4. Le cycle est toujours un intervalle élément de Z12, c'est-à-dire que chacune de ces échelles a un « pied », un passage dans l'échelle égalisée Z12 (de 12 1/2 tons par octave). Les 10 intervalles « passages » tonaux sont : la 4te, la 5te, la 6te M, la 7e m, la 7e M, l'8ve+2de m, l'8ve+2de M, l'8ve+3ce m, l'8ve+4te et l'8ve+5te. La prégnance de l'octave dans 7 échelles sur 11 reste forte (malgré la nonoctaviation numérique) : l'octave a une force d'attraction perceptive comparable à un trou noir qui aspire les petits intervalles autour d'elle et en + fait masque : les micro-intervalles satellitaires sont engloutis par sa présence (ou, nous donnons à l'octave une tolérance d'une marge d'1/2 ton : 1/4 au dessus et 1/4 en dessous). Nous verrons plus tard quoi faire avec les échelles 13/16e de ton (162.5 cents) et 15/16e de ton (187.5 cents).

. Pour 11 échelles nonoctaviantes de la famille Z96, il y a 7 nonoctaves telles que : { 1125 cents ; 1137,5 cents ; 1187,5 cents ; 1225 cents ; 1237,5 cents ; 1250 cents ; 1275 cents }.

. La famille nonoctaviante Z96 se caractérise par des cycles nonoctaviants de 4 et 8 horaires (3 échelles tétratoniques et 8 échelles octotoniques).

. Problème de conditionnement
Une révolution de cycle (l'intervalle divisé en horaires-notes) ne correspond pas à ce qu'on perçoit à l'écoute, par manque d'entrainement, l'échelle nonoctaviante inconnue est assimilée à notre perception conditionnée : la nonoctave est comprise comme une variation de l'octave et pas comme un autre ambitus différent. Cette approximation assimilante déplace le cycle constructeur chiffré au cycle assimilé octave de la nonoctave. Les 11 échelles nonoctaviantes de Z96, au lieu d'être 3 tétratoniques et 8 octotoniques, sont perçues en : 2 pentatoniques, 2 hexatoniques, 2 heptatoniques, 1 nonatonique, 1 décatonique, 1 hendécatonique, 1 tetradécatonique et 1 nanodécatonique.

. Pour s'introduire dans le monde des sonorités nonoctaviantes, nous conseillons d'abord la pratique des pentatoniques nonoctaviantes. La gamme pentatonique de 5 tons est la plus simple et se retrouve dans toutes les cultures sur la planète avec autant de variantes que de pratiques musicales. La densité du nombre de degrés de l'échelle, plus elle augmente, plus l'écoute se raffine et devient subtile, mais empêche un néophyte de comprendre le sens et la portée de la nonoctaviation : ne pas obligatoirement revenir au même point.

.

Téléchargez la famille des 11 échelles nonoctaviantes de Z96 (zip .scl files 5Ko)
Download the Z96 family of 11 nonoctave scales (.zip .scl scala files 5Ko)

Téléchargez la famille des 11 échelles nonoctaviantes de Z96 (.zip tuning script for Kontakt sampler .nkp 20Ko)
Download the Z96 family of 11 nonoctave scales (.zip tuning script for Kontakt sampler .nkp 20Ko)

.

Notation des 11 nonoctaves Z96 (encours)

... [en attendant la publication, voir la page de notation (globe) de toutes les échelles possible]

-> voir PASSAGES DE L'UNE A L'AUTRE Modes de correspondances entre elles

Entendons + loin... Suite des trouvailles des divisions non symétriques pour d’autres types d'échelles : celles multiples de 1/15 de ton :

EXPLORATION DE L'ECHELLE DE 1/15e DE TON
nommable aussi Z90 :

2. multiples de 1/15^e de ton

¹⁵√(⁶√2) = ⁹⁰√2 = 2^1/90 = 1,007731369217151530104557933693
Multiplions par les entiers naturels (1; 2; 3; ...; 15) 1/15 pour obtenir ses 15 échelles multiples :

nom rapport propriété

1 Echelle de 1/15^e de ton (2^1/90)¹ = 1,00773 symétrique octaviante = ⁹⁰√2

2 Echelle de 2/15^e de ton (2^1/90)² = 1,01552 asymétrique octaviante = ⁴⁵√2

3 Echelle de 1/5^e de ton (2^1/90)³ = 1,02337 symétrique octaviante = ³⁰√2

4 Echelle de 4/15^e de ton (2^1/90)⁴ = 1,031286 asymétrique nonoctaviante

5 Echelle de 1/3 de ton (2^1/90)⁵ = 1,03926 symétrique octaviante = ¹⁸√2

6 Echelle de 2/5^e de ton (2^1/90)⁶ = 1,04729 asymétrique octaviante = ¹⁵√2

7 Echelle de 7/15^e de ton (2^1/90)⁷ = 1,05539 asymétrique nonoctaviante

8 Echelle de 8/15^e de ton (2^1/90)⁸ = 1,06355 asymétrique nonoctaviante

9 Echelle de 3/5^e de ton (2^1/90)⁹ = 1,07177 symétrique octaviante = ¹⁰√2

10 Echelle de 10/15^e de ton (2^1/90)¹⁰ = 1,08006 asymétrique octaviante = ⁹√2

11 Echelle de 11/15^e de ton (2^1/90)¹¹ = 1,08841 asymétrique nonoctaviante

12 Echelle de 4/5^e de ton (2^1/90)¹² = 1,09825 asymétrique nonoctaviante

13 Echelle de 13/15^e de ton (2^1/90)¹³ = 1,1053 asymétrique nonoctaviante

14 Echelle de 14/15^e de ton (2^1/90)¹⁴ = 1,11385 asymétrique nonoctaviante

15 Echelle de ton (2^1/90)¹⁵ = 1,12246 symétrique octaviante = ⁶√2

16 Echelle de 16/15^e de ton (2^1/90)¹⁶ = 1,13114 asymétrique non-octaviante

17 Echelle de 17/15^e de ton (2^1/90)¹⁷ = 1,13988 asymétrique non-octaviante

18 Echelle de 6/5^e de ton (2^1/90)¹⁸ = 1,148698 asymétrique octaviante = ⁵√2

. remarque : contrairement à Z96, Z90 possède des échelles asymétriques nonoctaviantes et asymétriques octaviantes,
  mais Z90 n'a pas d'échelle symétrique non-octaviante.
  [rappel : une échelle symétrique est une échelle qui répète ses rapports par division binaire (= paire)]

Graphe des 18 premières échelles multiples de 1/15^e de ton :

. Le cycle de chaque échelle se répète tout les 5, 10 et 15 degrés sauf pour les 3 échelles 1/3 de ton (= ¹⁸√2); 10/15e de ton (= ⁹√2); 1 ton (= ⁶√2).
. Toutes les échelles multiples de 1/15e de ton répètent un cycle d'un intervalle inclus dans Z12.
. Des 18 échelles pentadecatoniques répétant un cycle de 15 degrés, 5 échelles reconnaissent un centre de symétrie dans leurs divisions de l'octave : 1/15e de ton (= ⁹⁰√2), 1/5e de ton (= ³⁰√2), 1/3 de ton (= ¹⁸√2), 3/5e de ton (= ¹⁰√2), 1 ton (= ⁶√2) qui divisent l'octave par un nombre pair.
. Des 17 échelles multiplent de Z90 (de 2/15e de ton à 6/5e de ton) 8 sont octaviantes et 9 sont nonoctaviantes.

Nous avons 9 échelles multiples de l’échelle d’1/15^e de ton qui ne sont pas symétriques dans l’octave et même l’ignore : elles sont nonoctaviantes,

telles les échelles :

nom quantification en cent rapport   (rappel : ¹²√2 = 1,05946)

4/15^e de ton 53,33.. cents (⁹⁰√2)⁴ = 1,03128...

7/15^e de ton 93,33.. cents (⁹⁰√2)⁷ = 1,05538...

8/15^e de ton 106,66.. cents (⁹⁰√2)⁸ = 1,06354...

11/15^e de ton 146,66.. cents (⁹⁰√2)¹¹ = 1,08839...

4/5^e de ton 160 cents (⁹⁰√2)¹² = 1,09681...

13/15^e de ton 173,33.. cents (⁹⁰√2)¹³ = 1,10529...

14/15^e de ton 186,66.. cents (⁹⁰√2)¹⁴ = 1,11383...

16/15^e de ton 213,33.. cents (⁹⁰√2)¹⁶ = 1,13114...

17/15^e de ton 226,66.. cents (⁹⁰√2)¹⁷ = 1,13988...

9 premières échelles nonoctaviantes asymétriques et cycliques multiples de l’échelle 1/15 de ton (13,33.. cents) ⁹⁰√2=1,00773 :

Graphe des 7 premières échelles asymétriques non-octaviantes multiples de l'échelle de 1/15^e de ton :

La symétrie n'apparait que par l'existence d'une division paire.
Ces 9 échelles divisent un cycle par un nombre impair 15 et donc ne reconnaissent pas un centre de symétrie dans leur cycle.

Propriétés de ces 9 échelles nonoctaviantes multiples de 1/15e de ton (13,33.. cents) ⁹⁰√2=1,00773 :

1. L'échelle de 4/15 de ton (53,33.. cents ou 1,03128) divise la 6te mineur (800 cents ou 1,58736) en 15 intervalles équidistants et reproduit les intervalles de 8ve + 3ce majeur (2 . 6te m), (3 . 6te m), etc. : 4/15e de ton est une échelle cyclique qui répète l'intervalle de 6te mineur et ses multiples : 15√1,58736 = 1,03128. Reste la prégnance de la quinte avec battement au 13e degré, même si celle-ci est plus petite (693,3 cents contre 700 cents). Reste la prégnance de l'octave avec battement au 22e degré, même si celle-ci est plus petite (1173,33.. cents contre 1200 cents), mais la nonoctave au 23e degré (1226,66.. cents contre 1200 cents) empêche la localisation exacte de l'octave. 1/4 de ton = 50 cents. Double octave exacte au 45e degré (2400 cents = 45 x 53,33.. cents). L'échelle de 4/15 de ton (53,33.. cents) est double octaviante.
00° : unisson
01° : 53,33 cents
02° : 106,66 cents
03° : 160 cents
04° : 213,33 cents
05° : 266,66 cents
06° : 320 cents
07° : 373,33 cents
08° : 426,66 cents
09° : 480 cents
10° : 533,33 cents
11° : 586,66 cents
12° : 640 cents
13° : 693,33 cents     [proche 5te : à 6,67 cents]
14° : 746,66 cents
15° : 800 cents          6m
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

2. L'échelle de 7/15e de ton (93,33.. cents ou 1,05538) divise l'octave + la seconde majeur (1400 cents ou 2,24483) en 15 intervalles équidistants et répète les intervalles d'8ve+2de M (2 . 8ve+2de M), (3 . 8ve+2de M), etc. : 7/15e de ton est une échelle cyclique qui répète l'intervalle de 8ve+2deM et ses multiples : 15√2,24483 = 1,05539. Reste la prégnance de l'octave avec battement au 13e degré, même si celle-ci est plus grande (1213.33 cents contre 1200 cents) et se répète tous les 13 degrés. (1/2 de ton = 100 cents).
00° : unisson
01° : 93,33 cents
02° : 186,66 cents
03° : 280 cents
04° : 373,33 cents
05° : 466,66 cents
06° : 560 cents
07° : 653,33 cents
08° : 746,66 cents
09° : 840 cents
10° : 933,33 cents
11° : 1026,66 cents
12° : 1120 cents
13° : 1213,33 cents       [proche 8ve : à 13,33 cents]
14° : 1306,66 cents
15° : 1400 cents            8ve+2deM
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

3. L'échelle de 8/15e de ton (106,66.. cents ou 1,06354) divise l'octave + 3ce majeur (1600 cents ou 2,51972) en 15 intervalles équidistants et répète les intervalles d'8ve+3ce M (2 . 8ve+3ce M), (3 . 8ve+3ce M), etc. : 8/15e de ton est une échelle cyclique qui répète l'intervalle de 8ve+3ceM et ses multiples : 15√2,51972 = 1,06355. Reste la prégnance de l'octave avec battement au 11e degré, même si celle-ci est plus petite (1173,33 cents contre 1200 cents). (1/2 de ton = 100 cents).
00° : unisson
01° : 106,66 cents
02° : 213,33 cents
03° : 320 cents
04° : 426,66 cents
05° : 533,33 cents
06° : 640 cents
07° : 746,66 cents
08° : 853,33 cents
09° : 960 cents
10° : 1066,66 cents
11° : 1173,33 cents      [proche 8ve : à 26,67 cents]
12° : 1280 cents
13° : 1386,66 cents
14° : 1493,33 cents
15° : 1600 cents           8ve+3ceM
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

4. L'échelle de 11/15e de ton (146,66.. cents ou 1,08839) divise l'octave + 7e mineur (2200 cents ou 3,56337) en 15 intervalles équidistants et répète les intervalles d'8ve+7e m (2 . 8ve+7e m), (3 . 8ve+7e m), etc. : 11/15e de ton est une échelle cyclique qui répète l'intervalle de 8ve+7em et ses multiples : 15√3,56337 = 1,08841. Entre 9√2 et 8 √2. Reste la prégnance de l'octave avec battement au 8e degré, même si celle-ci est plus petite (1173,33 cents contre 1200 cents). Ainsi que la prégnance de la quinte au 5e degré (733,33 contre 700 cents). Ainsi que la prégnance de l'8ve+5te au 13e degré (1906,66 contre 1900 cents).
00° : unisson
01° : 146,66 cents
02° : 293,33 cents
03° : 440 cents
04° : 586,66 cents
05° : 733,33 cents        [proche 5te : à 33,33 cents]
06° : 880 cents
07° : 1026,66 cents
08° : 1173,33 cents       [proche 8ve : à 26,67 cents]
09° : 1320 cents
10° : 1466,66 cents
11° : 1613,33 cents
12° : 1760 cents
13° : 1906,66 cents       [très proche 8ve+5te : à 6,66 cents]
14° : 2053,33 cents
15° : 2200 cents           8ve+7m
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

5. L'échelle de 4/5e de ton (160 cents ou 1,09681, est incluse dans l'échelle de 4/15 de ton) divise la 6te mineur (800 cents ou 1,58736) en 5 intervalles équidistants et répète l'intervalle de 6te m : (2 . 6te m), (3 . 6te m), etc. : 4/5e de ton est une échelle cyclique : 5√1,58736 = 1,09682. Double octave juste au 15e degré (2400 cents = 15 . 160). Au 10e degré 8ve+3M (1600 cents). Prégnance au 12e degré de l'8ve+5te (1920 cents contre 1900 cents). L'échelle de 4/5e de ton (160 cents) est double octaviante. Les 3 degrés 10, 12 et 15 forment l'accord tonal 3m+3M bien caractéristique.
00° : unisson
01° : 160 cents
02° : 320 cents
03° : 480 cents
04° : 640 cents
05° : 800 cents             6m
06° : 960
07° : 1120
08° : 1280
09° : 1440
10° : 1600
11° : 1760
12° : 1920
13° : 2080
14° : 2240
15° : 2400                   2x8ve
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

6. L'échelle de 13/15e de ton (173,33.. cents ou 1,10529) divise dbl8ve+2deM (2600 cents ou 4,48998) en 15 intervalles équidistants et répète l'intervalle de double octave + 2de majeur : (2 . (2 . 8ve+2deM)), (3 . (2 . 8ve+2deM)), (4 . (2 . 8ve+2deM)) : 13/15e de ton est une échelle cyclique : 15√4,48998 = 1,10531. Reste la prégnance de l'octave avec battement au 7e degré, même si celle-ci est plus grande (1213,33 cents contre 1200 cents). Aussi la prégance de la 5te au 4e degré et 8ve+5te au 11e degré et double 8ve au 14e degré.
00° : unisson
01° : 173,33 cents
02° : 346,66 cents
03° : 520 cents
04° : 693,33 cents        [proche 5te : à 6,67 cents]
05° : 866,66 cents
06° : 1040 cents
07° : 1213,33 cents      [proche 8ve : à 13,33 cents]
08° : 1386,66 cents
09° : 1560 cents
10° : 1733,33 cents
11° : 1906,66 cents      [proche 8ve+5te : à 6,66 cents]
12° : 2080 cents
13° : 2253,33 cents
14° : 2426,66 cents      [proche double 8ve : à 26,66 cents]
15° : 2600 cents           2x8ve+2M
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

7. L'échelle de 14/15e de ton (186,66.. cents ou 1,11383) divise dbl8ve+3ceM (2800 cents ou 5,0383) en 15 intervalles équidistants et répète l'intervalle de double octave + 3ce majeur : (2 . (2 . 8ve+3ceM)), (3 . (2 . 8ve+3ceM)), (4 . (2 . 8ve+3ceM)) : 14/15e de ton est une échelle cyclique : 15√5,0383 = 1,11383. Prégnance de la double octave au 13e degré : l'échelle de 14/15 de ton (186,66.. cents) est quasi double octaviante.
00° : unisson
01° : 186,66 cents
02° : 373,33 cents
03° : 560 cents
04° : 746,66 cents
05° : 933,33 cents
06° : 1120 cents
07° : 1306,66 cents
08° : 1493,33 cents
09° : 1680 cents
10° : 1866,66 cents
11° : 2053,33 cents
12° : 2240 cents
13° : 2426,66 cents      [proche double 8ve : à 26,66 cents]
14° : 2613,33 cents
15° : 2800 cents          2x8ve+3M
téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler .nkp

8. L'échelle de 16/15e de ton (213,33.. cents ou 1,13114... = (⁹⁰√2)¹⁶ divise 2x8ve+6te m (3200 cents) en 15. Prégance au 17e degré de la triple 8ve (3626,66.. contre 3600 cents). Les degrés 8 et 9 sont respectivement proches de l'8ve+4te et de l'8ve+5te. L'échelle de 16/15 de ton (213,33.. cents) est quasi triple octaviante.
00° : unison
01° : 213,33 cents
02° : 426,66 cents
03° : 640 cents
04° : 853,33 cents
05° : 1066,66 cents
06° : 1280 cents
07° : 1493,33 cents
08° : 1706,66 cents    [proche 8ve+4te : à 6,66 cents]
09° : 1920 cents         [proche 8ve+5te : à 20 cents]
10° : 2133,33 cents
11° : 2346,66 cents
12° : 2560 cents
13° : 2773,33 cents
14° : 2986,66 cents
15° : 3200 cents          2x8ve+6m

9. L'échelle de 17/15e de ton (226,66.. cents ou ) divise une dbl8ve+7e m (3400 cents) en 15. Prégance au 16e degré de la triple 8ve (3626,66.. contre 3600 cents). Et prégnance au 7e degré de l'8ve et 3ce majeure (1586,66 contre 1600 cents). L'échelle de 17/15 de ton (226,66.. cents) est quasi triple octaviante.
00° : unison
01° : 226,66 cents
02° : 453,33 cents
03° : 680 cents
04° : 906,66 cents
05° : 1133,33 cents
06° : 1360 cents
07° : 1586,66 cents       [proche 8ve+3M : à 13,34 cents]
08° : 1813,33 cents
09° : 2040 cents
10° : 2266,667 cents
11° : 2493,33 cents
12° : 2720 cents
13° : 2946,66 cents
14° : 3173,33 cents
15° : 3400 cents          2x8ve+7m

Récapitulation :

rang nom en ton ambitus (intervalle) divisé divisant par nonoctave proche octave au intervalle en cents nombre de degrés par 8ve désignation par densité

1 4/15^e de ton 800 cents 6te m 15 22e degré : 1173 contre 1200 53,33 cents 22,5 (45 degrés pour dbl 8ve) cycle de 22 tons

2 7/15^e de ton 1400 cents 8ve+2de M 15 13e degré : 1213 contre 1200 cents 93,33 cents 12,85... tridécatonique

3 8/15^e de ton 1600 cents 8ve+3ce M 15 11e degré : 1173 contre 1200 cents 106,66 cents 11,25 hendécatonique

4 11/15^e de ton 2200 cents 8ve+7e m 15 8e degré : 1173 contre 1200 cents 146,66 cents 8,18.. octotonique

5 4/5^e de ton 800 cents 6te m 5 15e degré : dbl 8ve 2400 cents 160 cents 7,5 (14 degrés pour dbl 8ve) tétradécatonique

6 13/15^e de ton 2600 cents 2x8ve+2de M 15 7e degré : 1213 contre 1200 cents 173,33 cents 6,92... heptatonique

7 14/15^e de ton 2800 cents 2x8ve+3ce M 15 6e degré : 1120 contre 1200 cents 186,66 cents 6,42... (quasi dbl 8ve) hexatonique

8 16/15^e de ton 3200 cents 2x8ve+6te m 15 17e degré : 3626,66.. contre 3600 cents 213,33 cents 5,62... (quasi trpl 8ve) heptadécatonique

9 17/15^e de ton 3400 cents 2x8ve+7e m 15 16e degré : 3626,66.. contre 3600 cents 226,66 cents 5,29... (quasi trpl 8ve) hexadecatonique

Remarques :

. Les 9 échelles nonoctaviantes de l'ensemble Z90 (1/15e de ton) sont toutes cycliques et divisent le cycle en nombre d'intervalles impairs par 15 ou 5. Le cycle est toujours un intervalle élément de Z12, c'est-à-dire que chacune de ces échelles a un « pied », un passage dans l'échelle tempérée Z12. Les 8 intervalles « passages » sont la 6te mineur, l'8ve+2de M, l'8ve+3ce M, l'8ve+7e m, la double 8ve+2deM, la double 8ve+3ceM, la double 8ve+6te m, la double 8ve+7e m. La prégnance de l'octave dans 5 échelles sur 9 reste forte (malgré leur nonoctaviation numérique). Les échelles de 4/15e de ton et de 4/5e de ton rencontrent la double octave. Les échelles de 7/15e de ton et 8/15e de ton cernent l'échelle d' 1/2 ton. L'échelle de 4/15e de ton (53,33.. cents) taquine l'échelle d'1/4 de ton (50 cents). 6 échelles sur 9 "taquinent" une nonoctave de 1173 cents et 1213 cents.

. Pour 9 échelles nonoctaviantes de la famille Z90, il y a 3 nonoctaves telles que : { 1120 cents, 1173 cents ; 1213 cents }, 2 échelles double octaviante (2400 cents), une échelle quasi double octaviante (2426,66 cents au 13e degré) et 2 échelles quasi triple octaviante (3626,66 cents au 16e at 17e degré).

. La famille nonoctaviante Z90 se caractérise par des cycles nonoctaviants de 5 et 15 horaires (1 échelle pentatonique et 8 échelles pentadécatoniques).

. Les 2 échelles 11/15e (146,66 cents) et 13/15e de ton (173,33 cents) qui entourent l'échelle centrale de 4/5e de ton (160 cents) sont truffées de 5te et d'8ve ! 16/15 (213,33 cents) est incluse dans 8/15 (106,66 cents) qui est incluse dans 4/15 (53,33 cents) est en fait la même échelle dont la densité se raréfie une fois sur deux. Même chose pour 14/15 (186,66 cents) qui est incluse dans 7/15 (93,33 cents). Cela réduit la famille de 9 à 6, mais est-ce vraiment à réduire ?

. Problème de déconditionnement contextuel
Le choix du cycle (l'intervalle divisé en horaires-notes) se fait par la prégnance, en général un intervalle connu (d'où la pioche dans Z12). Le cycle reprend à l'intervalle connu. Mais une révolution de cycle ne correspond pas à ce que l'on perçoit à l'écoute, par manque de déconditionnement, l'échelle nonoctaviante inconnue est assimilée à une perception conditionnée : la nonoctave est comprise comme une variation de l'octave et pas comme un autre cycle différent (même chose pour la quinte et la quarte). Elles sont augmentées et diminuées. Cette approximation assimilante déplace le cycle constructeur chiffré au cycle assimilé octave de la nonoctave : une large marge de tolérance ou d'intolérance qui perturbe la perception des fréquences voisines mais différentes. Les 9 échelles nonoctaviantes de Z90 au lieu d'être 1 pentatonique et 8 pentadécatoniques, sont perçues comme : 1 hexadecatonique, 1 heptadécatonique, 1 hexatonique, 1 heptatonique, 1 tétradécatonique, 1 octotonique, 1 hendécatonique, 1 tridécatonique et 1 cycle de 22 tons. Tout en ne l'étant pas vraiment. Toute la subtilité de la nonoctaviation se trouve en partie ici : d'être ou de ne pas être ? ce qui est.

. « Plus la densité du nombre de degrés de l'échelle augmente, plus l'écoute se raffine et devient subtile » ici ne se vérifie pas, les échelles éloignées par l'écart semblent être plus proches par leurs dispositions (17/15 (226,66 cents), 16/15 (213,33 cents) avec 4/15 (53,33 cents)). L'échelle centrale 4/5 (160 cents) regroupe les autres qui lui sont périphériques. « Bizarre, bizarre, vous avez dit bizarre ? Comme c'est bizarre ».

. Peut-on dire que les 9 échelles nonoctaviantes de Z90 ne sont pas totalement nonoctaviantes, mais quasi nonoctaviantes ? C'est un champ que je n'avais pas prévu : la quasinonoctaviation !

.

Téléchargez la famille des 9 échelles nonoctaviantes de Z90 (zip .scl files 5Ko)
Download the Z90 family of 9 nonoctave scales (.zip .scl scala files 5Ko)

Téléchargez la famille des 9 échelles nonoctaviantes de Z90 (.zip tuning script for Kontakt sampler .nkp 17Ko)
Download the Z90 family of 9 nonoctave scales (.zip tuning script for Kontakt sampler .nkp 17Ko)

.

Notation des 9 échelles nonoctaviantes Z90 (encours)

... [en attendant la publication, voir la page de notation (globe) de toutes les échelles possible]

-> voir PASSAGES DE L'UNE A L'AUTRE Modes de correspondances entre elles

PARENTHESE [ & anticipation :

Suitons les échelles non-octaviantes (mais cycliques) de Z96 et Z90 du plus petit au plus grand intervalle avant le ton, ceLA nous donne :

Suite des 15 échelles cycliques nonoctaviantes de Z96 (1/16e de ton) et de Z90 (1/15e de ton) - (rappel 100 cents = 1/2 ton : 1.05946) :

n° nom quantification en cent rapports exemples musicaux

01 4/15e de ton 53,33.. cents 1,03128 chopin 4/15 download .scl file

02 5/16e de ton 62,5 cents 1,03678 chopin 5/16 download .scl file

03 7/16e de ton 87,5 cents 1,05187 chopin 7/16 download .scl file

04 7/15e de ton 93,33.. cents 1,05538 chopin 7/15 download .scl file

05 8/15e de ton 106,66.. cents 1,06354 chopin 8/15 download .scl file

06 9/16e de ton 112,5 cents 1,06717 chopin 9/16 download .scl file

07 5/8e de ton 125 cents 1,07491 chopin 5/8 download .scl file

08 11/16e de ton 137,5 cents 1,0827 chopin 11/16 download .scl file

09 11/15e de ton 146,66.. cents 1,08839 chopin 11/15 download .scl file

10 4/5e de ton 160 cents 1,09681 chopin 4/5 download .scl file

11 13/16e de ton 162,5 cents 1,09846 chopin 13/16 download .scl file

12 13/15e de ton 173,33.. cents 1,10529 chopin 13/15 download .scl file

13 7/8e de ton 175 cents 1,10642 chopin 7/8 download .scl file

14 14/15e de ton 186,66.. cents 1,11383 chopin 14/15 download .scl file

15 15/16e de ton 187,5 cents 1,11445 chopin 15/16 download .scl file

Nous constatons que les 4 premières échelles sont microtonales et que les 11 autres sont macrotonales (nous nous sommes arrêtés avant le ton : 200 cents) montre que la frontière est arbitraire. Les échelles de 7/15e et de 8/15e cernent et sont proches de l'échelle de 1/2 ton mais ne reproduit pas ses proportions (sa sonorité). Afin de donner à ces échelles à une perception concrète, nous nous sommes amusés à interpréter ces échelles avec une musique bien connue de tous : la Valse op 64 n°2 de Frédérique Chopin déclinée dans ces 15 échelles (écoutez les exemples ci-dessus dans le tableau ou téléchargez le tout dans le conteneur 45Mo.zip). Les échelles sont construites sur l'origine du do3 médian à 261.63Hz accordées au diapason la3 à 440Hz.

Disponibles aussi à l'écoute, 4 récentes (2010) interprétations de « 3 Ephémérôdes partis du Milieu de la bombe » pour trois pianos, écrit à Rio de Janeiro en 2000 pour le trio du pianiste Waldemar Reis. Les quatre interprétations proposent ici : 1. un accord pour les trois pianos en 8/15e de ton, 2. un accord pour chacun de 4/15e de ton, 7/15e de ton et 11/15e de ton en deux interprétations : l'une résonnante et l'autre pas, et 3. un accord pour chacun de 1/2 ton, 9/16e de ton et 8/15e de ton. Téléchargez le tout dans un conteneur 122Mo.zip.

FIN DE LA PARENTHESE ]

Entendons + loin... Suite des trouvailles des divisions non symétriques pour d’autres échelles : celles multiples de 1/14 de ton :

EXPLORATION DE L'ECHELLE DE 1/14e DE TON
nommable aussi Z84 :

3. multiples de 1/14^e de ton

¹⁴√(⁶√2) = ⁸⁴√2 = 2^1/84 = 1,0082858916953740285765551729555
Multiplions par les entiers naturels (1; 2; 3; ...; 14) par 1/14 pour obtenir ses 17 échelles multiples :

nom formule rapport* quant. en cents propriété remarques

Echelle de 1/14^e de ton (⁸⁴√2)¹ = 1,00829 <=> 14,2857... symétrique octaviante = ⁸⁴√2 1,0082858916953740285765551729555 **

Echelle de 1/7^e de ton (⁸⁴√2)² = 1,01665 <=> 28,5714... symétrique octaviante = ⁴²√2 1,0166404393919355254466878281669

Echelle de 3/14^e de ton (⁸⁴√2)³ = 1,02508 <=> 42,8571... symétrique octaviante = ²⁸√2 1,0250642119658745674433761912354

Echelle de 2/7^e de ton (⁸⁴√2)⁴ = 1,03357 <=> 57,1428... symétrique octaviante = ²¹√2 1,0335577830070277304532462255542

Echelle de 5/14^e de ton (⁸⁴√2)⁵ = 1,04214 <=> 71,4285... asymétrique nonoctaviante 1,0421217308579348537980091159494

Echelle de 3/7^e de ton (⁸⁴√2)⁶ = 1,05078 <=> 85,7142... symétrique octaviante = ¹⁴√2 1,0507566386532194247355350853237

Echelle de 1/2^e de ton (⁸⁴√2)⁷ = 1,05949 <=> 100 cents symétrique octaviante = ¹²√2 = 1,05946 <=> 1/2 ton

Echelle de 4/7^e de ton (⁸⁴√2)⁸ = 1,06828 <=> 114,2857... asymétrique nonoctaviante 1,0682416908144022200136068970692

Echelle de 9/14^e de ton (⁸⁴√2)⁹ = 1,07713 <=> 128,5714... asymétrique nonoctaviante 1,0770930257689735860738394072839

Echelle de 5/7^e de ton (⁸⁴√2)¹⁰ = 1,08606 <=> 142,857... asymétrique nonoctaviante 1,0860177019263380088706088742993

Echelle de 11/14^e de ton (⁸⁴√2)¹¹ = 1,09507 <=> 157,1428... asymétrique nonoctaviante 1,09501632698375864013523791702

Echelle de 6/7^e de ton (⁸⁴√2)¹² = 1,10414 <=> 171,4285... symétrique octaviante = ⁷√2 1,1040895136738123376495053876233

Echelle de 13/14^e de ton (⁸⁴√2)¹³ = 1,1133 <=> 185,714285... asymétrique nonoctaviante 1,113237879806111729266212869331

Echelle de ton (⁸⁴√2)¹⁴ = 1,12253 <=> 200 cents symétrique octaviante = ⁶√2 6√2 = 1,12246 ou 1,1224620483093729814335330496792

Echelle de 15/14^e de ton (⁸⁴√2)¹⁵ = 1,13183 <=> 214,2857... asymétrique nonoctaviante

Echelle de 8/7^e de ton (⁸⁴√2)¹⁶ = 1,14121 <=> 228,5714... asymétrique nonoctaviante

Echelle de 17/14^e de ton (⁸⁴√2)¹⁷ = 1,15068 <=> 242,8571... asymétrique nonoctaviante

* calculé avec une calculette de poche
** calculé avec un ordinateur 32 bit

remarques :
. la division paire du ton retrouve toujours l'échelle de 1/2 ton au milieu <=> 12√2 = 1,0594630943592952645618252949463 et une symétrie des échelles nonoctaviantes.

Parenthèse + Attention [
Nous ne faisons pas cette exploration d'échelles afin d'enquiquiner les élèves des conservatoires de musique à jouer des gammes avec leur instrument de musique : comme si jouer des gammes permettait d'améliorer sa technique instrumentale ! Et ça agace tellement son entourage... Autant jouer des petites combinaisons (de la musique) pour se familiariser avec ces échelles où improviser avec celles-ci, etc. ]

Graphe des 14 premières échelles multiples de 1/14^e de ton :

. Le cycle de chaque échelle se répète tout les 7 degrés.
. Toutes les échelles multiples de 1/14e de ton répètent un cycle d'un intervalle de Z12
. Nous avons 6 échelles multiples de l’échelle d’1/14e de ton qui ignorent l’octave : nonoctaviantes
. Des 17 échelles multiplent de Z84 (de 1/14e de ton à 17/14e de ton) 8 sont octaviantes et 9 sont nonoctaviantes.

ne sont pas symétriques dans et même l’

telles que les échelles de :

nom quantification en cent rapport

5/14^e de ton 71,428571428571428571428571428571 cents (⁸⁴√2)⁵ = 1,04214...

4/7^e de ton 114,28571428571428571428571428571 cents (⁸⁴√2)⁸ = 1,06828...

9/14^e de ton 128,57142857142857142857142857143 cents (⁸⁴√2)⁹ = 1,07713...

5/7^e de ton 142,85714285714285714285714285714 cents (⁸⁴√2)¹⁰ = 1,08606...

11/14^e de ton 157,14285714285714285714285714286 cents (⁸⁴√2)¹¹ = 1,09507...

13/14^e de ton 185,71428571428571428571428571429 cents (⁸⁴√2)¹³ = 1,1133...

15/14^e de ton 214,2857... cents (⁸⁴√2)¹⁵= 1,13183

8/7^e de ton 228,5714... cents (⁸⁴√2)¹⁶= 1,14121

17/14^e de ton 242,8571... cents (⁸⁴√2)¹⁷= 1,15068

parenthèse [
Anticipation : nous constatons que pour chaque série d'échelles nous avons :
8 échelles nonoctaviantes multiples de 1/16e de ton
7 échelles nonoctaviantes multiples de 1/15e de ton
6 échelles nonoctaviantes multiples de 1/14e de ton
Donc les prochaines seront au nombre de :
5 échelles nonoctaviantes multiples de 1/13e de ton en fait 8 non 7
4 échelles nonoctaviantes multiples de 1/12e de ton
3 échelles nonoctaviantes multiples de 1/11e de ton
2 échelles nonoctaviantes multiples de 1/10e de ton
1 échelles nonoctaviantes multiples de 1/9e de ton
ce qui nous donne 36 (non) échelles nonoctaviantes multiples jusqu'à 1/16e de ton = fausse Anticipation ]

9 échelles nonoctaviantes asymétriques et cycliques multiples de l’échelle 1/14e de ton (14,28... cents) ⁸⁴√2=1,00829 :

Graphe des 6 premières échelles asymétriques nonoctaviantes multiples de l'échelle de 1/14^e de ton :

En considérant ces échelles heptatoniques, répétant un cycle de 7 degrés, elles ne reconnaissent pas un centre de symétrie dans leurs divisions. Elles sont asymétriques car elles ne possèdent pas un degrés central où l'image miroir correspond à l'image projetée. L'asymétrie apparait par l'effacement d'une division pair de 14 degrés pour 7 degrés. Ces 9 échelles divisent un cycle par un nombre impair 7 et donc ne reconnaissent pas un centre de symétrie dans son cycle. Elles sont toutes asymétriques.

Propriétés de ces 6 échelles non octaviantes multiples de 1/14e de ton (14,28... cents) ⁸⁴√2=1,00829 :

1. L'échelle 5/14e de ton (71,428 cents) divise l'intervalle de quarte (500 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que : septième mineur (2 x 4te) et octave+3ce mineure (3 x 4te), etc. : 5/14e de ton est une échelle cyclique qui répète l'intervalle de 4te et ses multiples. Sensation d'octave au 17e degré bien qu'il soit plus grand : 1214,293 cents (contre 1200) en plus de la quarte au 7e degré.
0° : unisson
1° : 71,429 cents
2° : 142,85 cents
3° : 214,28 cents
4° : 285,71 cents
5° : 357,14 cents
6° : 428,57 cents
7° : 500 cents            4te
...
10° : 714,28 cents       [proche 5te : à 14,28 cents]
...
17° : 1214,28 cents     [proche 8ve : à 14,28 cents]
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

2. L'échelle de 4/7e de ton (114,2857... cents) divise l'intervalle de 6te mineur (800 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que : octave+3ce majeure (2 x 6te m), etc. Sensation de quinte au 6e degré bien qu'il soit plus petit : 685,714 cents (contre 700 cents) en plus de la sixte mineur au 7e degré.
0° : unisson
1° : 114,28 cents
2° : 228,57 cents
3° : 342,85 cents
4° : 457,14 cents
5° : 571,43 cents
6° : 685,71 cents     [proche 5te : à 14,29 cents]
7° : 800 cents           6m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

3. L'échelle de 9/14e de ton (128,57... cents) divise l'intervalle de 6te majeur (900 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que : octave+triton (2 x 6te M), etc. Aucun degré qui puisse vraiment l'arrêter... Tout est entre Z12 bien que le 3e degré soit proche d'une 3ce majeure 385 cents contre 400.
0° : unisson
1° : 128,57 cents
2° : 257,14 cents
3° : 385,71 cents
4° : 514,28 cents
5° : 642,85 cents
6° : 771,43 cents
7° : 900 cents          6M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

4. L'échelle de 5/7e de ton (142,857... cents) divise l'intervalle de 7e mineur (1000 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que : Aucun degré qui puisse vraiment l'arrêter... Tout est entre Z12.
0° : unisson
1° : 142,85 cents
2° : 285,71 cents
3° : 428,57 cents
4° : 571,43 cents
5° : 714,28 cents   [proche 5te : à 14,286 cents]
6° : 857,14 cents
7° : 1000 cents        7m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

5. L'échelle de 11/14e de ton (157,142857... cents) divise l'intervalle de 7e majeur (1100 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que : octave+7e m (2 x 7e M), etc. Aucun degré qui puisse vraiment l'arrêter... Tout est entre Z12 bien que le 12e degré à 1885,716 cents soit proche d'un octave (1200 cents) + quinte (700 cents) = 1900 cents et que le 23e degré à 3614,289 cents soit proche du triple octave = 3600 cents.
0° : unisson
1° : 157,14 cents
2° : 314,28 cents
3° : 471,43 cents
4° : 628,57 cents
5° : 785,71 cents
6° : 942,85 cents
7° : 1100 cents       7M
...
12° : 1885.714       [proche 8ve+5te : à 14,28 cents]
...
23° : 3614.286       [proche triple 8ve : à + 14,28 cents]
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

6. L'échelle de 13/14e de ton (185,7142857... cents) divise l'intervalle d'octave + 2de mineur (1300 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que : double 8ve + 2de m (2600 cents), triple 8ve + 3ce m (3900 cents), etc. Au 13e degré on rencontre une double octave un peu haute à 2414,282 cents contre 2400 cents.
0: unisson
1: 185,71 cents
2: 371,42 cents
3: 557,14 cents
4: 742,85 cents
5: 928,57 cents
6: 1114,28 cents
7: 1300 cents            8ve+2m
...
13: 2414,28 cents     [proche double 8ve : à 14,28 cents]
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

7. L'échelle de 15/14e de ton (214,2857... cents) divise l'intervalle d'octave + 3ce mineure (1500 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que :
0° : unisson
1° : 214,28 cents
2° : 428,57 cents
3° : 642,85 cents
4° : 857,14 cents
5° : 1071,43 cents
6° : 1285,71 cents
7° : 1500 cents         8ve+3m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp
variante d'hexatonique = gamme par ton nonoctaviante

8. L'échelle de 8/7e de ton (228,5714... cents) divise l'intervalle d'octave + 3ce majeur (1600 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que :
0° : unisson
1° : 228,57 cents
2° : 457,14 cents
3° : 685,71 cents        [proche 5te : à 14,29 cents]
4° : 914,28 cents
5° : 1142,85 cents
6° : 1371,43 cents
7° : 1600 cents         8ve+3M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp
38 hauteurs couvrent tout l'ambitus du piano !

9. L'échelle de 17/14e de ton (242,8571...cents) divise l'intervalle d'octave + 4te (1700 cents) en 7 intervalles équidistants et reproduit les intervalles de Z12 tels que :
0° : unisson
1° : 242,85 cents
2° : 485,71 cents
3° : 728,57 cents
4° : 971,43 cents
5° : 1214,29 cents      [proche 8ve : à 14,29 cents]
6° : 1457,14 cents
7° : 1700 cents          8ve+4te
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp
35 notes couvrent tout l'ambitus du piano ! variante de pentatonique

n° nom ambitus (intervalle) divisé division par nonoctaviation

1 5/14^e de ton 500 cents 4te 7 au 17e degré : 1214 contre 1200 cents

2 4/7^e de ton 800 cents 6te m 7

3 9/14^e de ton 900 cents 6te M 7

4 5/7^e de ton 1000 cents 7e m 7

5 11/14^e de ton 1100 cents 7e M 7 Trpl 8ve au 23e degré : 3614 contre 3600 cents

6 13/14^e de ton 1300 cents 8ve+2de m 7 Dbl 8ve au 13e degré : 2414 contre 2400 cents

7 15/14^e de ton 1500 cents 8ve+3ce m 7

8 8/7^e de ton 1600 cents 8ve+3ce M 7

9 17/14^e de ton 1700 cents 8ve+4te 7

Remarques :
Les 9 échelles nonoctaviantes de l'ensemble Z84 (1/14e de ton) sont toutes cycliques et divisent le cycle-ambitus en nombre d'intervalles impairs par 7. Les cycles-ambitus sont des intervalles éléments de Z12, c'est-à-dire que chacune de ces échelles a un « pied », un passage dans l'échelle tempérée Z12. Les 9 intervalles « passages » sont la 4te, la 6te mineur, la 6te majeur, la 7e mineur, la 7e majeur, l'8ve+2de mineur, l'8ve+3ce mineur, l'8ve+3ce majeur, l'8ve+4te. La prégnance de l'octave dans 4 dont 2 échelles sur 9 reste présente malgré leur nonoctaviation numérique. L'échelle de 5/14e de ton rencontre l'octave au 17e degré et une 5te au 10e degré, l'échelle de 13/14e de ton rencontre la double octave au 13e degré, l'échelle de 11/14e de ton rencontre une triple octave au 23e degré et une octave + quinte au 12e degré, l'échelle de 4/7e de ton rencontre une quinte au 6e degré, l'échelle de 17/14e de ton rencontre l'octave au 5e degré.

-> voir PASSAGES DE L'UNE A L'AUTRE Modes de correspondances entre elles

.

Téléchargez la famille des 9 échelles nonoctaviantes de Z84 (zip .scl files 5Ko)
Download the Z84 family of 9 nonoctave scales (.zip .scl scala files 5Ko)

Téléchargez la famille des 9 échelles nonoctaviantes de Z84 (.zip tuning script for Kontakt sampler .nkp 17Ko)
Download the Z84 family of 9 nonoctave scales (.zip tuning script for Kontakt sampler .nkp 17Ko)

.

Notation des 9 nonoctaves Z84 (en cours)

... [en attendant la publication, voir la page de notation (globe) de toutes les échelles possible]

...

Entendons + loin... Suite des trouvailles des divisions non symétriques pour d’autres échelles : celles multiples de 1/13 de ton :

EXPLORATION DE L'ECHELLE DE 1/13e DE TON
nommable aussi Z78 :

4. multiples de 1/13^e de ton

¹³√(⁶√2) = ⁷⁸√2 = 2^1/78 = 1,0089261044979412419235679603889...
Multiplions par les entiers naturels (1; 2; 3; ...; 13) 1/13 pour obtenir ses 13 échelles multiples :

nom rapport propriété

1 Echelle de 1/13^e de ton (2^1/78)¹ = 1,00892... symétrique octaviante = ⁷⁸√2

2 Echelle de 2/13^e de ton (2^1/78)² = 1,01793... asymétrique octaviante = ⁴⁹√2

3 Echelle de 3/13^e de ton (2^1/78)³ = 1,02701... symétrique octaviante = ²⁶√2

4 Echelle de 4/13^e de ton (2^1/78)⁴ = 1,03618... asymétrique nonoctaviante

5 Echelle de 5/13e de ton (2^1/78)⁵ = 1,04543... asymétrique nonoctaviante

6 Echelle de 6/13^e de ton (2^1/78)⁶ = 1,05476... asymétrique octaviante = ¹³√2

7 Echelle de 7/13^e de ton (2^1/78)⁷ = 1,06418... asymétrique nonoctaviante

8 Echelle de 8/13^e de ton (2^1/78)⁸ = 1,07368... asymétrique nonoctaviante

9 Echelle de 9/13^e de ton (2^1/78)⁹ = 1,08326... asymétrique nonoctaviante

10 Echelle de 10/13^e de ton (2^1/78)¹⁰ = 1,09293... asymétrique nonoctaviante

11 Echelle de 11/13^e de ton (2^1/78)¹¹ = 1,10268... asymétrique nonoctaviante

12 Echelle de 12/13e de ton (2^1/78)¹² = 1,11253... asymétrique double-octaviante

13 Echelle de ton (2^1/78)¹³ = 1,12246... symétrique octaviante = ⁶√2

14 Echelle de 14/13^e de ton (2^1/78)¹⁴ = 1,13248... asymétrique nonoctaviante

15 Echelle de 15/13^e de ton (2^1/78)¹⁵ = 1,14258... asymétrique nonoctaviante

16 Echelle de 16/13^e de ton (2^1/78)¹⁶ = 1,15278... asymétrique nonoctaviante

17 Echelle de 17/13^e de ton (2^1/78)¹⁷ = 1,16307... asymétrique nonoctaviante

18 Echelle de 18/13^e de ton (2^1/78)¹⁸ = 1,17346... asymétrique nonoctaviante

Remarque :
. Dans ce tableau Z78 possède 12 échelles asymétriques nonoctaviantes (8 jusqu'au ton), 2 échelles asymétriques octaviantes, 3 échelles symétriques octaviantes et aucune échelle symétrique nonoctaviante.

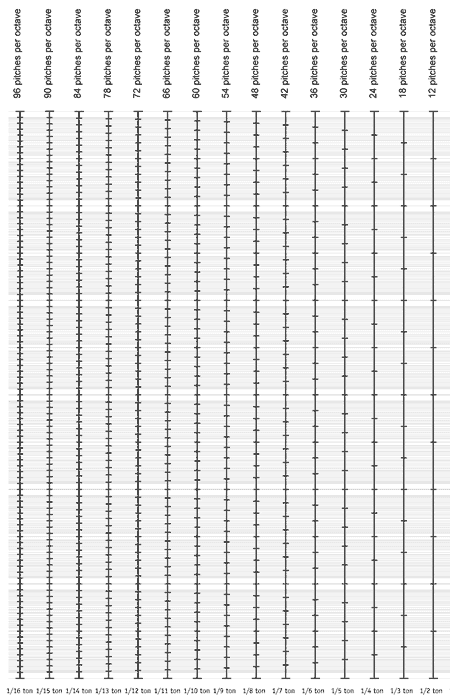
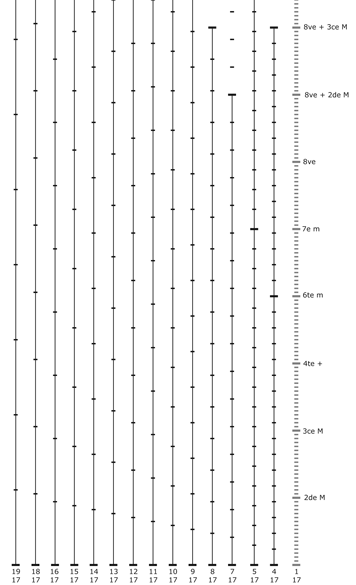
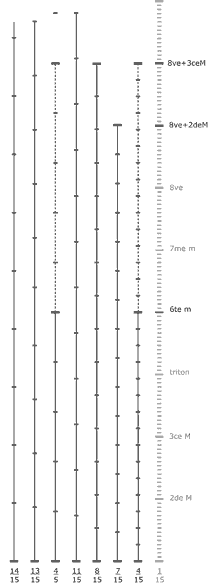
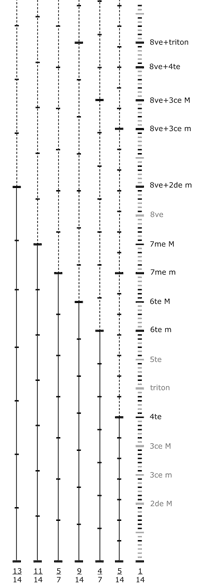
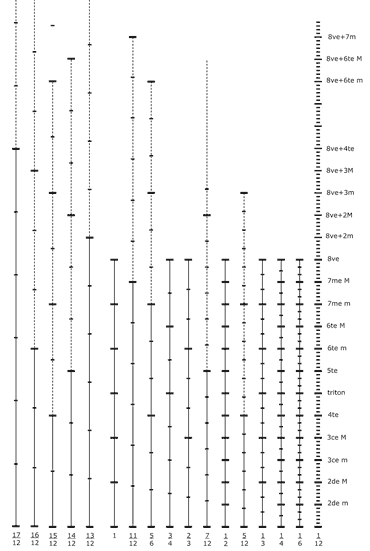
Graphe des 17 premières échelles multiples de 1/13^e de ton :

. Nous avions anticipé 5 échelles nonoctaviantes multiples de 1/13e de ton dont l'intervalle est inférieur au ton, nous nous sommes trompés : il y en a 8.
. 13 est un nombre premier (qui ne se divise que par 1 ou par lui-même).
. Le cycle de chaque échelle se répète tout les 13 degrés.
. Toutes les échelles multiples de 1/13e de ton (Z78) répètent un cycle d'un intervalle inclus dans Z12.
. Des 13 échelles multiplent de Z78 (de 1/13e de ton à 13/13e de ton) 5 sont octaviantes et 8 sont nonoctaviantes : inégalité !

Nous avons 8 premières échelles multiples de l’échelle d’1/13e de ton qui ignorent l’octave : nonoctaviantes

telles que les échelles de :

nom quantification en cent rapport

4/13^e de ton 61,5384... cents (⁷⁸√2)⁴ = 1,03618...

5/13^e de ton 76,923... cents (⁷⁸√2)⁵ = 1,04543...

7/13^e de ton 107,6923... cents (⁷⁸√2)⁷ = 1,06418...

8/13^e de ton 123,0769... cents (⁷⁸√2)⁸ = 1,07368...

9/13^e de ton 138,4615... cents (⁷⁸√2)⁹ = 1,08326...

10/13^e de ton 153,846... cents (⁷⁸√2)¹⁰ = 1,09293...

11/13^e de ton 169,2307 cents (⁷⁸√2)¹¹ = 1,10268...

12/13^e de ton 184,6153... cents (⁷⁸√2)¹² = 1,11253...

et

14/13^e de ton 215,3846... cents (⁷⁸√2)¹⁴ = 1,13248...

15/13^e de ton 230,76923... cents (⁷⁸√2)¹⁵ = 1,14258...

16/13^e de ton 246,1538... cents (⁷⁸√2)¹⁶ = 1,15278...

17/13^e de ton 261,5384... cents (⁷⁸√2)¹⁷ = 1,16307...

8 échelles cycliques asymétriques nonoctaviantes et multiples de l’échelle 1/13e de ton (15,384615384615384615384615384615 cents) ⁷⁸√2=1,0089261 aux intervalles inférieurs au ton et 4 supérieurs au ton.

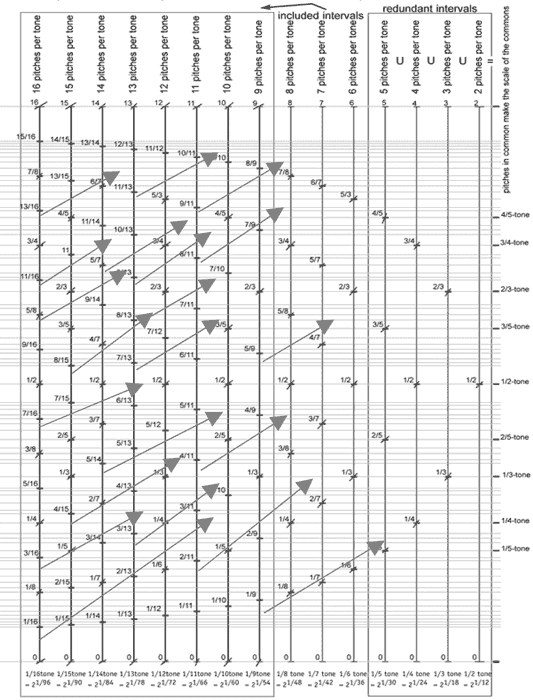
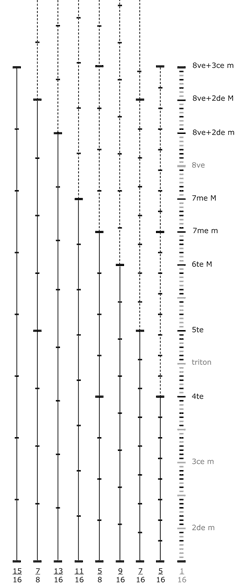
Graphe des 8 + 4 premières échelles asymétriques nonoctaviantes multiples de l'échelle de 1/13^e de ton :

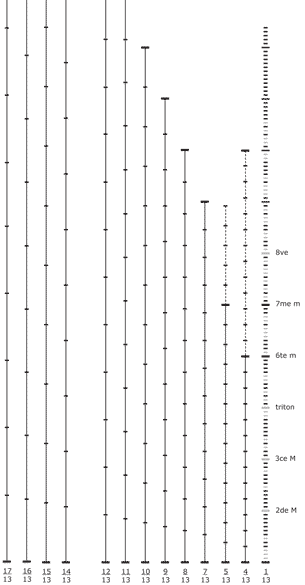
En considérant ces échelles treizotoniques, répétant un cycle de 13 degrés, elles ne reconnaissent pas un centre de symétrie dans leurs divisions. Elles sont asymétriques. Elles ne possèdent pas un degrés central où l'image miroir correspond à l'image projetée. Ces 8 + 4 échelles divisent un cycle par un nombre impair et premier 13 et donc ne reconnaissent pas un centre de symétrie dans son cycle.

Propriétés de ces 8 échelles non octaviantes multiples de 1/13e de ton (15,3846... cents) ⁷⁸√2 = 1,00892... :

1. L'échelle 4/13e de ton (61,5384... cents) divise l'intervalle de 6te mineure (800 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : sixte mineur, octave + 3ce majeure (2 x 6te m), etc. : 4/13e de ton est une échelle cyclique qui répète l'intervalle de 6te m et ses multiples. Le 8e degrés s'assimile à une quarte bien qu'il soit plus bas de 8 cents (492,308 cents contre 500 cents) et le 19e degrés s'assimile à l'octave bien qu'il sonne plus bas de 30 cents (1169,23 cents contre 1200 cents).
00° : unisson
01° : 61,54 cents
02° : 123,07 cents
03° : 184,61 cents
04° : 246,15 cents
05° : 307,69 cents
06° : 369,23 cents
07° : 430,77 cents
08° : 492,31 cents
09° : 553,84 cents
10° : 615,38 cents
11° : 676,92 cents
12° : 738,46 cents
13° : 800 cents          6m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

2. L'échelle 5/13e de ton (76,923 cents) divise l'intervalle de 7e mineur (1000 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : 7e mineur, octave + 6te mineur (2 x 7e m), etc. : 5/13e de ton est une échelle cyclique qui répète l'intervalle de 7e m et ses multiples. Le 4e degré s'assimile à la 3ce mineure (307,7 cents contre 300 cents). Le 9e degrés s'assimile à la quinte bien qu'il soit plus bas de 8 cents (692,308 cents contre 700 cents) et le 16e degrés s'assimile à l'octave bien qu'il sonne plus haut de 30 cents (1230,77 cents contre 1200 cents).
00° : unisson
01° : 76,92 cents
02° : 153,84 cents
03° : 230,77 cents
04° : 307,69 cents
05° : 384,61 cents
06° : 461,54 cents
07° : 538,46 cents
08° : 615,38 cents
09° : 692,31 cents
10° : 769,23 cents
11° : 846,15 cents
12° : 923,07 cents
13° : 1000 cents         7m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

Ici, il est intéressant de comparer l'échelle de 5/13e de ton de 76,923 cents à une échelle proche qui divise l'octave en 16 intervalles égaux de 75 cents :

rang 5/13e de ton 8ve div 16 différence

01 76,923 75 1,923

02 153,846 150 3,846

03 230,769 225 5,769

04 307,692 300 7,692

05 384,615 375 9,615

06 461,538 450 11,538

07 538,462 525 13,462

08 615,385 600 15,385

09 692,308 675 17,308

10 769,231 750 19,231

11 846,154 825 21,154

12 923,077 900 23,077

13 1000 975 25

14 1076,923 1050 26,923

15 1153,846 1125 28,846

16 1230,769 1200 30,769

3. L'échelle 7/13e de ton (107,7 cents) divise l'intervalle d'8ve+2de majeur (1400 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : 8ve+2deM (1400 cents), double octave+3ceM (2800 cents), etc. : 7/13e de ton est une échelle cyclique qui répète l'intervalle de 8ve+2deM et ses multiples. 7/13e de ton (107,7 cents) est proche d'1/2 ton (100 cents), mais la sensation d'octave se fait au 11e degré à 1184,6 cents contre 1200 cents, une différence de 15,4 cents. Le 6e degré est intéressant comme un triton augmenté...
00° : unisson
01° : 107,69 cents
02° : 215,38 cents
03° : 323,07 cents
04° : 430,77 cents
05° : 538,46 cents
06° : 646,15 cents
07° : 753,84 cents
08° : 861,54 cents
09° : 969,23 cents
10° : 1076,92 cents
11° : 1184,61 cents
12° : 1292,31 cents
13° : 1400 cents           8ve+2M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

4. L'échelle 8/13e de ton (123,077 cents) divise l'intervalle d'8ve+3ce majeur (1600 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : 8ve+3ceM (1600 cents), double octave+6tem (3200 cents), etc. : 8/13e de ton est une échelle cyclique qui répète l'intervalle de 8ve+3ceM et ses multiples. Le 4eme degré est proche de la quarte (492,308 cents contre 400 cents) et le dixième degré proche de l'octave bien qu'il soit plus grand (1230,77 contre 1200 cents) avec une différence de 30,77 cents.
00° : unisson
01° : 123,07 cents
02° : 246,15 cents
03° : 369,23 cents
04° : 492,31 cents
05° : 615,38 cents
06° : 738,46 cents
07° : 861,54 cents
08° : 984,61 cents
09° : 1107,69 cents
10° : 1230,77 cents
11° : 1353,84 cents
12° : 1476,92 cents
13° : 1600 cents         8ve+3M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

5. L'échelle de 9/13e de ton (138,4615... cents) divise l'intervalle d'8ve+4te augmentée ou quinte diminuée ou triton (1800 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : 8ve + 4te+ (1800 cents), triple octave (3600 cents), quadruple octave + 4te+ (5400 cents) etc. : 9/13e de ton est une échelle cyclique qui répète l'intervalle d'8ve + 4te+ et ses multiples. Le 5eme degré est proche de la quinte (692,308 cents contre 700 cents).
00° : unisson
01° : 138,46 cents
02° : 276,92 cents
03° : 415,38 cents
04° : 553,84 cents
05° : 692,31 cents
06° : 830,77 cents
07° : 969,23 cents
08° : 1107,69 cents
09° : 1246,15 cents
10° : 1384,61 cents
11° : 1523,07 cents
12° : 1661,54 cents
13° : 1800 cents           8ve+4+
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

6. L'échelle de 10/13e de ton (153,846... cents) divise l'intervalle d'8ve+6te mineur (2000 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : 8ve+6te majeur (2000 cents), triple octave + 3ce M (4000 cents), etc. : 10/13e de ton est une échelle cyclique qui répète l'intervalle d'8ve+6teM et ses multiples. Le second degré est proche de la tierce mineure (307,692 cents contre 300 cents), le quatrième degré est proche de la quarte augmentée (615,385 cents contre 600 cents). Il est intéressant de noter la présence de l'octave au 8eme degré, mais résolument faux où il peut garder sa fonction tout en n'étant pas à sa place.
00° : unisson
01° : 153,84 cents
02° : 307,69 cents
03° : 461,54 cents
04° : 615,38 cents
05° : 769,23 cents
06° : 923,07 cents
07° : 1076,92 cents
08° : 1230,77 cents
09° : 1384,61 cents
10° : 1538,46 cents
11° : 1692,31 cents
12° : 1846,15 cents
13° : 2000 cents           8ve+6m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

Ici, il est intéressant de comparer l'échelle de 20/13e de ton de 307,692 cents à l'échelle de tierce mineur qui divise l'octave en 4 intervalles égaux de 300 cents :

rang 20/13e de ton tierce mineure différence

01 307,692 300 7,692

02 615,385 600 15,385

03 923,077 900 23,077

04 1230,769 1200 30,769

05 1538,46 1500 38,46

06 1846,152 1800 46,152

07 2153,844 2100 53,844

08 2461,536 2400 61,536

7. L'échelle de 11/13e de ton (169,2307cents) divise l'intervalle d'8ve+7e mineur (2200 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que : 8ve+7e m (2200 cents), triple 8ve + 6te m (4400 cents), etc. : 11/13e de ton est une échelle cyclique qui répète l'intervalle d'8ve+7e m et ses multiples. Malgré que le 3e degré soit proche de la quarte (507,692 cents contre 500 cents) et que le 6e degré soit proche de la 7e mineur (1015,385 cents contre 1000 cents), cette échelle semble offrir la sensation d'une échelle heptatonique (7) divisant l'octave (1184,615 cents contre 1200 cents).
00° : unisson
01° : 169,23 cents
02° : 338,46 cents
03° : 507,69 cents
04° : 676,92 cents
05° : 846,15 cents
06° : 1015,38 cents
07° : 1184,61 cents
08° : 1353,84 cents
09° : 1523,07 cents
10° : 1692,31 cents
11° : 1861,54 cents
12° : 2030,77 cents
13° : 2200 cents          8ve+7m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

Ici, il est intéressant de comparer l'échelle de 11/13e de ton de 307,692 cents au mode majeur qui divise l'octave en 7 intervalles inégaux :

degré 11/13e de ton mode Majeur différence

01 169,231 200 30,769

02 338,462 400 61,538

03 507,692 500 7,692

04 676,923 700 23,077

05 846,154 900 53,846

06 1015,385 1100 84,615

07 1184,615 1200 15,385

pour mémoire 1/4 de ton <=> 50 cents et 1/8e de ton <=> 25 cents

8. L'échelle de 12/13e de ton (184,6153... cents) divise l'intervalle de double 8ve (2400 cents) en 13 intervalles équidistants et reproduit les intervalles de Z12 tels que la double octave (4), la quadruple octave (8) et l'octuple octave (16). 12/13e de ton est une échelle (double) octaviante.
00° : unisson
01° : 184,61 cents
02° : 369,23 cents
03° : 553,84 cents
04° : 738,46 cents
05° : 923,07 cents
06° : 1107,69 cents
07° : 1292,31 cents
08° : 1476,92 cents
09° : 1661,54 cents
10° : 1846,15 cents
11° : 2030,77 cents
12° : 2215,38 cents
13° : 2400 cents           2x8ve
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

9. L'échelle de 14/13e de ton divise l'intervalle de double 8ve+3ce Majeure (2800 cents) en 13 intervalles équidistants
00° : unisson
01° : 215,38 cents
02° : 430,77 cents
03° : 646,15 cents
04° : 861,54 cents
05° : 1076,92 cents
06° : 1292,31 cents
07° : 1507,69 cents
08° : 1723,07 cents
09° : 1938,46 cents
10° : 2153,84 cents
11° : 2369,23 cents
12° : 2584,61 cents
13° : 2800 cents            2x8ve+3M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

10. L'échelle de 15/13e de ton divise l'intervalle de double 8ve+4te+ (3000 cents) en 13 intervalles équidistants
00° : unisson
01° : 230,77 cents
02° : 461,54 cents
03° : 692,31 cents
04° : 923,07 cents
05° : 1153,84 cents
06° : 1384,61 cents
07° : 1615,38 cents
08° : 1846,15 cents
09° : 2076,92 cents
10° : 2307,69 cents
11° : 2538,.46 cents
12° : 2769,23 cents
13° : 3000 cents            2x8ve+4+
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

11. L'échelle de 16/13e de ton divise l'intervalle de double 8ve+6te mineure (3200 cents) en 13 intervalles équidistants
00° : unisson
01° : 246,15 cents
02° : 492,31 cents
03° : 738,46 cents
04° : 984,61 cents
05° : 1230,77 cents
06° : 1476,92 cents
07° : 1723,07 cents
08° : 1969,23 cents
09° : 2215,38 cents
10° : 2461,54 cents
11° : 2707,69 cents
12° : 2953,84 cents
13° : 3200 cents            2x8ve+6m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

Récapitulation :

rang nom ambitus (intervalle) divisé division par nonoctaviation

1 4/13^e de ton 800 cents 6te m 13 au 19e degré : 1169 contre 1200 cents

2 5/13^e de ton 1000 cents 7e m 13 au 16e degré : 1230 contre 1200 cents

3 7/13^e de ton 1400 cents 8ve+2deM 13 au 11e degré : 1184 contre 1200 cents

4 8/13^e de ton 1600 cents 8ve+3ce M 13 au 10e degré : 1230 contre 1200 cents

5 9/13^e de ton 1800 cents 8ve+4te+ 13 au 9e degré : 1246,154 contre 1200 cents

6 10/13^e de ton 2000 cents 8ve+6te M 13 au 8e degré : 1230,769 contre 1200 cents

7 11/13^e de ton 2200 cents 8ve+7e m 13 au 7e degré : 1184 contre 1200 cents

8 12/13^e de ton 2400 cents Dbl 8ve 13 au 6e degré : 1107,692 contre 1200 cents
ou au 7e degré : 1292,308 contre 1200 cents

9 14/13^e de ton 2800 cents Dbl 8ve+3ce M 13 au 6e degré : 1292,307 cents contre 1200 cents

10 15/13^e de ton 3000 cents Dbl 8ve+4te+ 13 au 5e degré : 1153,846 cents contre 1200 cents

11 16/13^e de ton 3200 cents Dbl 8ve+6te m 13 au 5e degré : 1230,769 cents contre 1200 cents

Remarques :
Les 11 échelles nonoctaviantes de l'ensemble Z78 (1/13e de ton) sont toutes cycliques et divisent le cycle en nombre d'intervalles impairs par 13. Les cycles sont tous des intervalles éléments de Z12, c'est-à-dire que chacune de ces échelles a un « pied », un passage dans l'échelle tempérée Z12. Les 11 intervalles tonaux « passages » sont la 6te mineure, la 7e mineure, l'8ve + 2de majeure, l'8ve + 3ce majeure, l'8ve + 4te augmentée, l'8ve + 6te majeure et l'8ve + 7e mineure, la double octave (= échelle quasioctaviante), la double octave + la 3ce majeure, la double octave + la 4te+, la double octave + la 6te mineure. La prégnance de l'octave dans 5 échelles sur 7 reste importante malgré leur nonoctaviation numérique et une division première. L'échelle de 4/13e de ton rencontre une octave au 19e degré, l'échelle de 5/13e de ton rencontre une octave au 16e degré, l'échelle de 7/13e de ton rencontre une octave au 11e degré, l'échelle de 8/13e de ton rencontre une octave au 10e degré, l'échelle de 11/13e de ton rencontre une octave au 7e degré.

-> voir PASSAGES DE L'UNE A L'AUTRE Modes de correspondances entre elles

.

Téléchargez la famille des 11 échelles nonoctaviantes de Z78 (zip .scl files 6Ko)
Download the Z78 family of 11 nonoctave scales (.zip .scl scala files 6Ko)

Téléchargez la famille des 11 échelles nonoctaviantes de Z78 (.zip tuning script for Kontakt sampler .nkp 21Ko)
Download the Z78 family of 11 nonoctave scales (.zip tuning script for Kontakt sampler .nkp 21Ko)

.

Entendons + loin... Suite des trouvailles des divisions non symétriques pour d’autres échelles : celles multiples de 1/12 de ton :

EXPLORATION DE L'ECHELLE DE 1/12e DE TON
nommable aussi Z72 :

5. multiples de 1/12^e de ton

¹²√(⁶√2) = ⁷²√2 = 2^1/72 = 1,0096735332285108621925214011186
Multiplions par les entiers naturels (1; 2; 3; ...; 12) 1/12 pour obtenir ses 12 échelles multiples :

nom rapport propriété

1 Echelle de 1/12^e de ton (2^1/72)¹ = 1,00967... symétrique octaviante = ⁷²√2

2 Echelle de 1/6^e de ton (2^1/72)² = 1,01943... symétrique octaviante = ³⁶√2

3 Echelle de 1/4^e de ton (2^1/72)³ = 1,02929... symétrique octaviante = ²⁴√2

4 Echelle de 1/3^e de ton (2^1/72)⁴ = 1,03924... symétrique octaviante = ¹⁸√2

5 Echelle de 5/12e de ton (2^1/72)⁵ = 1,04929... asymétrique nonoctaviante

6 Echelle de 1/2 ton (2^1/72)⁶ = 1,05944... symétrique octaviante = ¹²√2

7 Echelle de 7/12^e de ton (2^1/72)⁷ = 1,06969... asymétrique nonoctaviante

8 Echelle de 2/3 de ton (2^1/72)⁸ = 1,08003... asymétrique octaviante = ⁹√2

9 Echelle de 3/4 de ton (2^1/72)⁹ = 1,09047... symétrique octaviante = ⁸√2

10 Echelle de 5/6^e de ton (2^1/72)¹⁰ = 1,10102... asymétrique nonoctaviante

11 Echelle de 11/12^e de ton (2^1/72)¹¹ = 1,11167... asymétrique nonoctaviante

12 Echelle de ton (2^1/72)¹² = 1,1224... symétrique octaviante = ⁶√2

13 Echelle de 13/12^e de ton (2^1/72)¹³ = 1,13327... asymétrique nonoctaviante

14 Echelle de 14/12^e de ton (2^1/72)¹⁴ = 1,14423... asymétrique nonoctaviante

15 Echelle de 15/12^e de ton (2^1/72)¹⁵ = 1,15529... asymétrique nonoctaviante

16 Echelle de 16/12^e de ton (2^1/72)¹⁶ = 1,16646... asymétrique nonoctaviante

17 Echelle de 17/12^e de ton (2^1/72)¹⁷ = 1,17774... asymétrique nonoctaviante

remarques :
. Dans ce tableau Z72 possède 4+5 échelles asymétriques nonoctaviantes (4 jusqu'au ton), 8 échelles symétriques octaviantes et aucune échelle symétrique nonoctaviante ni asymétriques octaviantes.
. la division paire retrouve toujours la 4+ <=> 12√2 = 1,0594630943592952645618252949463 et une symétrie des échelles nonoctaviantes.
. Ah l'échelle de 12eme de ton ! Z72 est la seule échelle à rassembler et Z12 (1/2 ton), et Z18 (1/3 de ton) et Z24 (1/4 de ton). Ses échelles multiples octaviantes micro-intervallaires sont : 1/6e de ton, 1/4 de ton, 1/3 de ton, et macro-intervallaires : 1/2 ton, 2/3 de ton et 3/4 de ton.
. C'est l'échelle microintervallaire retenue par Ivan Wyschnégradsky en 1924 pour figurer l'élargissement scalaire à l' « espace pansonique » [ici, son livre La loi de la pansonorité en publication libre éducative]. Pratique, car elle inclus les divisions binaires et ternaires de l'octave.

Graphe des 16 1ères échelles multiples de Z72

Nous avons 9 échelles nonoctaviantes incluant les 5 au-delà du ton.
Les 7 échelles octaviantes sont les + familières : par ton, 3/4 de ton, 2/3 de ton, 1/2 ton, 1/3 de ton, 1/4 de ton, 1/6e de ton.
Ivan Wyschnegradsky découvre ces 5 1ères échelles nonoctaviantes en 1924.

nom quantification en cent rapport

5/12^e de ton 83,33.. cents (⁷²√2)⁵ = 1,04929...

7/12^e de ton 116,66.. cents (⁷²√2)⁷ = 1,06969...

5/6^e de ton 166,66.. cents (⁷²√2)¹⁰ = 1,10102...

11/12^e de ton 183,33.. cents (⁷²√2)¹¹ = 1,11167...

et

13/12^e de ton 216,66.. cents (⁷²√2)¹³ = 1,13327...

14/12^e de ton 233,33.. cents (⁷²√2)¹⁴ = 1,14423...

15/12^e de ton 250 cents (⁷²√2)¹⁵ = 1,15529...

16/12^e de ton 266,66.. cents (⁷²√2)¹⁶ = 1,16646...

17/12^e de ton 283,33.. cents (⁷²√2)¹⁷ = 1,17774...

. Le cycle de chaque échelle se répète tous les 6 degrés voire 3 et 2, ce sont des échelles hexatoniques.
. Toutes les échelles multiples de 1/12e de ton (Z72) répètent un cycle d'un intervalle inclus dans Z12.
. Des 16 échelles multiples de Z72 (de 1/12e de ton à 17/12e de ton) 8 sont octaviantes et 9 sont nonoctaviantes : inégalité !

1.
L'échelle nonoctaviante de 5/12e de ton divise une 4te en 6 degrés et une 7m en 12 degrés, une 8ve+3m en 18 degrés, etc.
00° : unisson
01° : 83,33 cents
02° : 166,66 cents     2de m + 1/3 de ton
03° : 250 cents          2de M + 1/4 de ton
04° : 333,33 cents
05° : 416,66 cents
06° : 500 cents          4te
07° : 583,33 cents
08° : 666,66 cents      4te+ & 1/3 de ton
09° : 750 cents          5te + 1/4 de ton
10° : 833,33 cents      6m + 1/6e de ton
11° : 916,66 cents
12° : 1000 cents         7m
13° : 1083,33 cents
14° : 1166,66 cents     7M + 1/3 de ton
15° : 1250 cents          8ve+1/4 de ton
16° : 1333,33 cents
17° : 1416,66 cents
18° : 1500 cents          8ve+3m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

2.
L'échelle nonoctaviante de 7/12e de ton divise une 5te en 6 degrés et une 8ve+2M en 12 degrés.
00° : unison
01° : 116,66 cents
02° : 233,33 cents      2M + 1/6e de ton
03° : 350 cents          3m + 1/4 de ton
04° : 466,66 cents      3M + 1/3 de ton
05° : 583,33 cents
06° : 700 cents           5te
07° : 816,66 cents
08° : 933,33 cents       6M + 1/6e de ton
09° : 1050 cents         7m + 1/4 de ton
10° : 1166,66 cents     7M + 1/3 de ton
11° : 1283,33 cents
12° : 1400 cents          8ve+2M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

3.
L'échelle nonoctaviante de 5/6e de ton ou 10/12e de ton divise une 4te en 3 degrés, une 7m en 6 degrés, une 8ve+3m en 9 degrés, etc. 5/6 est inclus en totalité dans 5/12e. Cette inclusion complète rend son indépendance numérique impossible. Mais entendant les sonorités bien distinctes entre le chromatisme de 12 1/2 ton et l'échelle par ton...
00° : unisson
01° : 166,66 cents       2m + 1/3 de ton
02° : 333,33 cents       3m + 1/6e de ton
03° : 500 cents            4te
04° : 666,66 cents       4te+ & 1/3 de ton
05° : 833,33 cents       6m + 1/6e de ton
06° : 1000 cents          7m
07° : 1166,66 cents
08° : 1333,33 cents
09° : 1500 cents          8ve+3m
10° : 1666,66 cents
11° : 1833,33 cents
12° : 2000 cents          8ve+6m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

4.
L'échelle nonoctaviante de 11/12e de ton divise une 7M en 6 degrés, 8ve+7m (2200 cents) en 12 degrés.
0° : unisson
1° : 183,33 cents
2° : 366,66 cents
3° : 550 cents            4te+1/4 de ton
4° : 733,33 cents
5° : 916,66 cents
6° : 1100 cents          7M
7° : 1283,33 cents
8° : 1466,66 cents
9° : 1650 cents          8ve+3M+1/4 de ton
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

puis

5.
L'échelle nonoctaviante de 13/12e de ton divise une 8ve + 2m en 6 degrés.
0° : unisson
1° : 216,66 cents
2° : 433,33 cents
3° : 650 cents            4te+ & 1/4 de ton
4° : 866,66 cents
5° : 1083,33 cents
6° : 1300 cents           8ve+2m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

6.
L'échelle nonoctaviante de 14/12e de ton divise une 5te en 3 degrés ou une 8ve + 2M en 6 degrés
0° : unisson
1° : 233,33 cents       2M + 1/6e de ton
2° : 466,67 cents       3M + 1/3 de ton
3° : 700 cents            5te
4° : 933,33 cents       6M + 1/6e de ton
5° : 1166,66 cents     7M + 1/3 de ton
6° : 1400 cents          8ve+2M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

7. L'échelle nonoctaviante de 15/12e de ton divise une 4te en 2 degrés ou 7m en 4 degrés ou une 8ve+3m en 6 degrés. C'est l'échelle de 5/4 de ton. C'est l'une des échelles nonoctaviante la + simple de la collection tonale. Par simple on entend celle qui peut avoir le rôle de passeuse entre Z12 et toutes les autres. Un intervalle sur 2 fait partie de Z12. Un intervalle sur 2 fait partie de Z24 (échelle octaviante de 1/4 de ton). 15/12e de ton est totalement incluse dans 5/12e de ton.
0° : unisson
1° : 250 cents     2M + 1/4 de ton
2° : 500 cents     4te
3° : 750 cents     5te + 1/4 de ton
4° : 1000 cents   7m
5° : 1250 cents   8ve+1/4 de ton
6° : 1500 cents   8ve+3m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

8.
L'échelle nonoctaviante de 16/12e de ton divise une 6te m en 3 degrés ou une 8ve + 3M en 6 degrés.
0° : unisson
1° : 266,66 cents        2M + 1/3 de ton
2° : 533,33 cents        4te + 1/6e de ton
3° : 800 cents             6m
4° : 1066,66 cents      7m + 1/3 de ton
5° : 1333,33 cents      8ve + 3m + 1/6e de ton
6° : 1600 cents           8ve+3M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

9.
L'échelle nonoctaviante de 17/12e de ton divise une 8ve + 4te en 6 degrés.
0° : unisson
1° : 283,33 cents
2° : 566,66 cents         4te + 1/3 de ton
3° : 850 cents             6m+1/4 de ton
4° : 1133,33 cents       7M + 1/6 de ton
5° : 1416,66 cents
6° : 1700 cents           8ve+4te
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

La particularité de Z72 de détenir des intervalles familiers + que les autres
lui donne la fonction de passage vers d'autres intervalles moins familiers.

...

Téléchargez la famille des 9 échelles nonoctaviantes de Z72 (zip .scl files 5Ko)
Download the Z72 family of 9 nonoctave scales (.zip .scl scala files 5Ko)

Téléchargez la famille des 9 échelles nonoctaviantes de Z72 (.zip tuning script for Kontakt sampler .nkp 18Ko)
Download the Z72 family of 9 nonoctave scales (.zip tuning script for Kontakt sampler .nkp 18Ko)

-> comprendre les PASSAGES DE L'UNE A L'AUTRE
avec les modes scalaires de correspondances entre échelles

Entendons plus loin... Suite des trouvailles des divisions non symétriques pour d’autres échelles : celles multiples de 1/11 de ton :

EXPLORATION DE L'ECHELLE DE 1/11e DE TON
nommable aussi Z66 :

6. multiples de 1/11^e de ton

¹¹√(⁶√2) = ⁶⁶√2 = 2^1/66 = 1,0105575719944727895462310227068
Multiplions par les entiers naturels (1; 2; 3; ...; 11) 1/11 pour obtenir ses 11 échelles multiples :

nom rapport propriété

1 Echelle de 1/11^e de ton (2^1/66)¹ = 1,00967... symétrique octaviante = ⁶⁶√2

2 Echelle de 2/11^e de ton (2^1/66)² = 1,01943... asymétrique octaviante = ³³√2

3 Echelle de 3/11^e de ton (2^1/66)³ = 1,02929... symétrique octaviante = ²²√2

4 Echelle de 4/11^e de ton (2^1/66)⁴ = 1,03924... asymétrique nonoctaviante

5 Echelle de 5/11^e de ton (2^1/66)⁵ = 1,04929... asymétrique nonoctaviante

6 Echelle de 6/11^e de ton (2^1/66)⁶ = 1,05944... asymétrique octaviante = ¹¹√2

7 Echelle de 7/11^e de ton (2^1/66)⁷ = 1,06969... asymétrique nonoctaviante

8 Echelle de 8/11^e de ton (2^1/66)⁸ = 1,08003... asymétrique nonoctaviante

9 Echelle de 9/11^e de ton (2^1/66)⁹ = 1,09047... asymétrique nonoctaviante

10 Echelle de 10/11^e de ton (2^1/66)¹⁰ = 1,10102... asymétrique nonoctaviante

11 Echelle de ton (2^1/66)¹¹ = 1,1224... symétrique octaviante = ⁶√2

12 Echelle de 12/11^e de ton (2^1/66)¹³ = 1,13327... asymétrique nonoctaviante

13 Echelle de 13/11^e de ton (2^1/66)¹⁴ = 1,14423... asymétrique nonoctaviante

14 Echelle de 14/11^e de ton (2^1/66)¹⁵ = 1,15529... asymétrique nonoctaviante

15 Echelle de 15/11^e de ton (2^1/66)¹⁶ = 1,16646... asymétrique nonoctaviante

16 Echelle de 16/11^e de ton (2^1/66)¹⁷ = 1,17774... asymétrique nonoctaviante

Nous avons 6 échelles nonoctaviantes (+ 4 au-delà du ton) = 10

nom quantification en cent rapport

4/11^e de ton 72,72.. cents (⁶⁶√2)⁴ = 1,03924...

5/11^e de ton 90,90.. cents (⁶⁶√2)⁵ = 1,04929...

7/11^e de ton 127,27.. cents (⁶⁶√2)⁷ = 1,06969...

8/11^e de ton 145,45.. cents (⁶⁶√2)⁸ = 1,08003...

9/11^e de ton 163,63.. cents (⁶⁶√2)⁹ = 1,09047...

10/11^e de ton 181,81.. cents (⁶⁶√2)¹⁰ = 1,1224...

et

13/11^e de ton 236,36.. cents (⁶⁶√2)¹³ = 1,13327...

14/11^e de ton 254,54.. cents (⁶⁶√2)¹⁴ = 1,14423...

15/11^e de ton 272,72.. cents (⁶⁶√2)¹⁵ = 1,15529...

16/11^e de ton 290,90.. cents (⁶⁶√2)¹⁶ = 1,16646...

17/11^e de ton 309,09.. cents (⁶⁶√2)¹⁷ = 1,17774...

1. L'échelle nonoctaviante de 4/11e de ton divise une 6te mineure en 11 degrés.
00° : unisson
01° : 72,72 cents
02° : 145,45 cents
03° : 218,18 cents
04° : 290,91 cents
05° : 363,63 cents
06° : 436,36 cents
07° : 509,09 cents
08° : 581,82 cents
09° : 654,54 cents
10° : 727,27 cents
11° : 800 cents          6te m
téléchargez le Scala tuning script .scl

2. L'échelle nonoctaviante de 5/11e de ton divise une 7e mineure en 11 degrés.
00° : unisson
01° : 90,91 cents
02° : 181,81 cents
03° : 272,72 cents
04° : 363,63 cents
05° : 454,54 cents
06° : 545,45 cents
07° : 636,36 cents
08° : 727,27 cents
09° : 818,18 cents
10° : 909,09 cents
11° : 1000 cents       7e m
téléchargez le Scala tuning script .scl

3. L'échelle nonoctaviante de 7/11e de ton divise une 8ve + ton = 1400 cents en 11 degrés.
00° : unisson
01° : 127,27 cents
02° : 254,54 cents
03° : 381,82 cents
04° : 509,09 cents
05° : 636,36 cents
06° : 763,63 cents
07° : 890,91 cents
08° : 1018,18 cents
09° : 1145,45 cents
10° : 1272,72 cents
11° : 1400                  8ve + ton
téléchargez le Scala tuning script .scl

4. L'échelle nonoctaviante de 8/11e de ton divise une 8ve + 3M = 1600 cents en 11 degrés [16/11e]
00° : unisson
01° : 145,45 cents
02° : 290,91 cents
03° : 436,36 cents
04° : 581,81 cents
05° : 727,27 cents
06° : 872,72 cents
07° : 1018,18 cents
08° : 1163,63 cents
09° : 1309,09 cents
10° : 1454,54 cents
11° : 1600 cents        8ve + 3M
téléchargez le Scala tuning script .scl
Tous les intervalles de 8/11e de ton sont inclus dans l'échelle 4/11e de ton

5. L'échelle nonoctaviante de 9/11e de ton divise une 8ve + 4+ = 1800 cents en 11 degrés
00° : unisson
01° : 163,63 cents
02° : 327,27 cents
03° : 490,91 cents
04° : 654,54 cents
05° : 818,18 cents
06° : 981,81 cents
07° : 1145,45 cents
08° : 1309,09 cents
09° : 1472,72 cents
10° : 1636,36 cents
11° : 1800 cents       8ve + 4+
téléchargez le Scala tuning script .scl

6. L'échelle nonoctaviante de 10/11e de ton divise une 8ve + 6te m = 2000 cents en 11 degrés
00° : unisson
01° : 181,81 cents
02° : 363,63 cents
03° : 545,45 cents
04° : 727,27 cents
05° : 909,09 cents
06° : 1090,91 cents
07° : 1272,72 cents
08° : 1454,54 cents
09° : 1636,36 cents
10° : 1818,18 cents
11° : 2000 cents        8ve + 6te m
téléchargez le Scala tuning script .scl

7. L'échelle nonoctaviante de 13/11e de ton divise 2 8ve + ton = 2600 cents en 11 degrés
00° : unisson
01° : 236,36 cents
02° : 472,72 cents
03° : 709,09 cents
04° : 945,45 cents
05° : 1181,81 cents
06° : 1418,18 cents
07° : 1654,54 cents
08° : 1890,91 cents
09° : 2127,27 cents
10° : 2363,63 cents
11° : 2600 cents         2x8ve + ton
téléchargez le Scala tuning script .scl
AUCUN INTERVALLE COMMUN AVEC SES SOEURS

8. L'échelle nonoctaviante de 14/11e de ton divise 2 8ve + 3M = 2800 cents en 11 degrés
00° : unisson
01° : 254,54 cents
02° : 509,09 cents
03° : 763,63 cents
04° : 1018,18 cents
05° : 1272,72 cents
06° : 1527,27 cents
07° : 1781,81 cents
08° : 2036,36 cents
09° : 2290,91 cents
10° : 2545,45 cents
11° : 2800 cents        2x8ve + 3M
téléchargez le Scala tuning script .scl
Tous les intervalles de 14/11e de ton sont inclus dans l'échelle 7/11e de ton

9. L'échelle nonoctaviante de 15/11e de ton divise 2 8ve + 4+ = 3000 cents en 11 degrés
00° : unisson
01° : 272,72 cents
02° : 545,45 cents
03° : 818,18 cents
04° : 1090,91 cents
05° : 1363,63 cents
06° : 1636,36 cents
07° : 1909,09 cents
08° : 2181,81 cents
09° : 2454,54 cents
10° : 2727,27 cents
11° : 3000 cents        2x8ve + 4+
téléchargez le Scala tuning script .scl

10. L'échelle nonoctaviante de 16/11e de ton divise 2 8ve + 6m = 3200 cents en 11 degrés
00° : unisson
01° : 290,91 cents
02° : 581,81 cents
03° : 872,72 cents
04° : 1163,63 cents
05° : 1454,54 cents
06° : 1745,45 cents
07° : 2036,36 cents
08° : 2327,27 cents
09° : 2618,18 cents
10° : 2909,09 cents
11° : 3200 cents         2x8ve + 6te m
téléchargez le Scala tuning script .scl
Tous les intervalles de 16/11e de ton sont inclus dans l'échelle 8/11e de ton

The 10 nonoctave Z66 scales [5Ko Scala] zipped

Remarques

Il existe des intervalles redondants [en gras] propres à l'échelle de 1/11e de ton qu'on retrouve dans ses 10 échelles nonoctaviantes, tels : 290,91 cents ; 545,45 cents ; 581,82 cents ; 727,27 cents ; 818,18 cents ; 872,72 cents ; 909,09 cents ; 1090,91 cents ; 1163,63 cents ; 13454,54 cents ; 2036,36 cents ; etc., ce qui est propice à sonner des ponts entre les échelles de cette famille. Tous les intervalles de l'échelle 14/11e de ton sont inclus dans l'échelle 7/11e de ton. Tous les intervalles de l'échelle 16/11e de ton sont inclus dans l'échelle 8/11e de ton. Ce qui fait 8 échelles distinctes avec des intervalles communs.

Ce tableau donne à voir les liens entre les 10 échelles nonoctaviantes :

Ou

Disposition ENSEMBLE

Les 10 échelles nonoctaviantes de Z66 [1/11e de ton] ensemble
sans l'échelle 13/11e de ton qui n'a aucun intervalle commun avec ses soeurs

4/11e de ton + 5/11e de ton + 7/11e de ton + 8/11e de ton + 9/11e de ton + 10/11e de ton + 14/11e de ton + 15/11e de ton + 16/11e de ton
limités dans leurs ambitus respectifs éléments de Z12

[intervalles en cents]

00° : unisson
01° : 72,72
01° : 90,91
01° : 127,27
02° : 145,45 01° : 145,45
01° : 163,63
02° : 181,81 01° : 181,81
03° : 218,18
02° : 254,54 01° : 254,54
03° : 272,72 01° : 272,72
04° : 290,91 02° : 290,91 01° : 290,91
02° : 327,27
05° : 363,63 04° : 363,63 02° : 363,63
03° : 381,82
06° : 436,36 03° : 436,36
05° : 454,54
03° : 490,91
07° : 509,09 04° : 509,09 02° : 509,09
06° : 545,45 03° : 545,45 02° : 545,45
08° : 581,82 04° : 581,81 02° : 581,81
07° : 636,36 05° : 636,36
09° : 654,54 04° : 654,54
10° : 727,27 08° : 727,27 05° : 727,27 04° : 727,27
06° : 763,63 03° : 763,63
11° : 800
09° : 818,18 05° : 818,18 03° : 818,18
06° : 872,72 03° : 872,72
07° : 890,91
10° : 909,09 05° : 909,09
06° : 981,81
11° : 1000
08° : 1018,18 07° : 1018,18 04° : 1018,18
06° : 1090,91 04° : 1090,91
09° : 1145,45 07° : 1145,45
08° : 1163,63 04° : 1163,63
10° : 1272,72 07° : 1272,72 05° : 1272,72
09° : 1309,09 08° : 1309,09
05° : 1363,63
11° : 1400
10° : 1454,54 08° : 1454,54 05° : 1454,54
09° : 1472,72
06° : 1527,27
11° : 1600
10° : 1636,36 09° : 1636,36 06° : 1636,36
06° : 1745,45
07° : 1781,81
11° : 1800
10° : 1818,18
07° : 1909,09
11° : 2000
08° : 2036,36 07° : 2036,36
08° : 2181,81
09° : 2290,91
08° : 2327,27
09° : 2454,54
10° : 2545,45
09° : 2618,18
10° : 2727,27
11° : 2800
10° : 2909,09
11° : 3000
11° : 3200

10.echelles.nonoctaviantes.de.Z66.[1,11e de ton].ensemble.txt

...

.

Entendons + loin...
suite de trouvailles des divisions non symétriques pour d’autres échelles : celles multiples de 1/10 de ton :

EXPLORATION DE L'ECHELLE DE 1/10e DE TON
nommable aussi Z60 :

7. multiples de 1/10^e de ton

¹⁰√(⁶√2) = ⁶⁰√2 = 2^1/60 = 1,0116194403019224846862305670455 = 20 cents
Multiplions par les entiers naturels (1; 2; 3; ...; 10) 1/10 pour obtenir ses 10 échelles multiples :

nom rapport propriété cents

1 Echelle de 1/10^e de ton (2^1/60)¹ = 1,0116194403019224846862305670455 symétrique octaviante = ⁶⁰√2 20

2 Echelle de 1/5^e de ton (2^1/60)² = 1,02337389199677490985454347065 symétrique octaviante = ³⁰√2 40

3 Echelle de 3/10^e de ton (2^1/60)³ = 1,0352649238413775043477881942112 symétrique octaviante = ²⁰√2 60

4 Echelle de 2/5^e de ton (2^1/60)⁴ = 1,047294122820626717891597012091 asymétrique octaviante = ¹⁵√2 80

5 Echelle de 1/2 ton (2^1/60)⁵ = 1,0594630943592952645618252949463 symétrique octaviante = ¹²√2 100

6 Echelle de 3/5^e de ton (2^1/60)⁶ = 1,0717734625362931642130063250233 symétrique octaviante = ¹⁰√2 120

7 Echelle de 7/10^e de ton (2^1/60)⁷ = 1,0842268703014183772867117824686 asymétrique nonoctaviante 140

8 Echelle de 4/5^e de ton (2^1/60)⁸ = 1,0968249796946259606814717780288 symétrique nonoctaviante échelle commune avec 12/15e de ton 160

9 Echelle de 9/10^e de ton (2^1/60)⁹ = 1,1095694720678450084893783577306 asymétrique nonoctaviante 180

10 Echelle de ton (2^1/60)¹⁰ = 1,1224620483093729814335330496792 symétrique octaviante = ⁶√2 200

11 Echelle de 11/10^e de ton (2^1/60)¹¹ = 1,1355044290708773728204827598732 asymétrique nonoctaviante 220

12 Echelle de 6/5^e de ton (2^1/60)¹² = 1,1486983549970350067986269467779 asymétrique nonoctaviante échelle commune avec 18/15e de ton 240

13 Echelle de 13/10^e de ton (2^1/60)¹³ = 1,1620455869578396167337137300698 asymétrique nonoctaviante 260

14 Echelle de 7/5^e de ton (2^1/60)¹⁴ = 1,1755479062836087076229542551622 asymétrique nonoctaviante échelle commune avec 21/15e de ton 280

15 Echelle de 15/10^e de ton (2^1/60)¹⁵ = 1,1892071150027210667174999705605 asymétrique nonoctaviante 300

16 Echelle de 8/5^e de ton (2^1/60)¹⁶ = 1,2030250360821166509571254425037 asymétrique nonoctaviante échelle commune avec 24/15e de ton 320

rapp el
Une division paire donne une échelle symétrique (avec une valeur centrale), une division impaire donne une échelle asymétrique (sans valeur centrale).

On a 3 échelles nonoctaviantes en dessous du ton pour 7 échelles octaviantes
mais une est commune avec l'échelle nonoctaviante de 12/15e de ton
Au-delà du ton, il y a 2 échelles nonoctaviantes
[Au-delà de 240 cents, on dépasse la densité 5 qui est le nombre limite de hauteurs pour constituer une gamme]
mais une est commune avec l'échelle nonoctaviante de 18/15e de ton

Ce qui fait 3 échelles nonoctaviantes pour Z60

nom quantification en cent rapport

7/10^e de ton 140 cents (2^1/60)⁷ = 1,08422...

9/10^e de ton 180 cents (2^1/60)⁹ = 1,10957...

11/10^e de ton 220 cents (2^1/60)¹¹ = 1,135504...

L'échelle de 1/10e de ton détient le taux le + pauvre d'échelles nonoctaviantes

1. L'échelle nonoctaviante de 7/10e de ton divise une 5te mineure en 5 degrés
00° : unisson
01° : 140 cents
02° : 280 cents
03° : 420 cents
04° : 560 cents
05° : 700 cents    5te
téléchargez le Scala tuning script .scl

2. L'échelle nonoctaviante de 9/10e de ton divise une 6te majeure en 5 degrés
00° : unisson
01° : 180 cents
02° : 360 cents
03° : 540 cents
04° : 720 cents
05° : 900 cents    6teM
téléchargez le Scala tuning script .scl

3. L'échelle nonoctaviante de 11/10e de ton divise une 7e majeure en 5 degrés
00° : unisson
01° : 220 cents
02° : 440 cents
03° : 660 cents
04° : 880 cents
05° : 1100 cents   7eM
téléchargez le Scala tuning script .scl
...

D'où, d'ailleurs ?

Qu'est-ce que c'est que ça : 1,0105575719944727895462310227068 = 18,181818 cents ?
Et ses multiples :

18,181818 1,01055...

36,363636 1,01943...

54,545454 1,02929...

72,727272 1,03924...

90,90909 1,04929...

109,090908 1,05944...

127,272726 1,06969...

145,454544 1,08003...

163,636362 1,09047...

181,81818 1,1224...

200 1,13327...

218,181816 1,13327...

236,363634 1,14423...

254,545452 1,15529...

272,72727 1,16646...

290,909088 1,17774...

.

.

Entendons encore + loin (dans le fait, + près : 1/9e de ton est + grand qu'1/16e de ton)
suite de trouvailles des divisions non symétriques pour d’autres échelles : celles multiples de 1/9 de ton :

EXPLORATION DE L'ECHELLE DE 1/9e DE TON
nommable aussi Z54 :

8. multiples de 1/9^e de ton

⁹√(⁶√2) = ⁵⁴√2 = 2^1/54 = 1,0129187947249466155952769436929...
Multiplions par les entiers naturels (1; 2; 3; ...; 9) 1/9 pour obtenir ses 9 échelles multiples :

nom rapport propriété

1 Echelle de 1/9^e de ton (2^1/54)¹ = 1,01292... symétrique octaviante = ⁵⁴√2

2 Echelle de 2/9^e de ton (2^1/54)² = 1,02601... asymétrique octaviante = ²⁷√2

3 Echelle de 3/9^e de ton (2^1/54)³ = 1,03926... symétrique octaviante = ¹⁸√2

4 Echelle de 4/9^e de ton (2^1/54)⁴ = 1,05269... asymétrique nonoctaviante

5 Echelle de 5/9e de ton (2^1/54)⁵ = 1,06629... asymétrique nonoctaviante

6 Echelle de 6/9^e de ton (2^1/54)⁶ = 1,08007... asymétrique octaviante = ⁹√2

7 Echelle de 7/9^e de ton (2^1/54)⁷ = 1,09402... asymétrique nonoctaviante

8 Echelle de 8/9^e de ton (2^1/54)⁸ = 1,10816.. asymétrique nonoctaviante

9 Echelle de ton (2^1/54)⁹ = 1,1224... symétrique octaviante = ⁶√2

10 Echelle de 10/9^e de ton (2^1/54)¹⁰ = 1,13698... asymétrique nonoctaviante

11 Echelle de 11/9^e de ton (2^1/54)¹¹ = 1,15167... asymétrique nonoctaviante

12 Echelle de 12/9^e de ton (2^1/54)¹² = 1,16655... asymétrique nonoctaviante

13 Echelle de 13/9^e de ton (2^1/54)¹³ = 1,18162... asymétrique nonoctaviante

14 Echelle de 14/9^e de ton (2^1/54)¹⁴ = 1,19688.. asymétrique nonoctaviante

15 Echelle de 15/9^e de ton (2^1/54)¹⁵ = 1,21235... asymétrique nonoctaviante

16 Echelle de 16/9^e de ton (2^1/54)¹⁶ = 1,22801... asymétrique nonoctaviante

...

Le n° du rang * localise le cycle

* XIe siècle, du francique hring = anneau

Propriétés des 5 échelles nonoctaviantes multiples de 1/9e de ton (22,22.. cents) ⁵⁴√2 = 1,0129187947249466155952769436929... :

1. L'échelle 4/9e de ton (88,88.. cents) divise l'intervalle de 6te mineure (800 cents) en 9 intervalles équidistants et reproduit les intervalles de Z12 tels que : sixte mineure, octave + 3ce majeure (2 x 6te m), etc. : 4/9e de ton est une échelle cyclique qui répète l'intervalle de 6te m et ses multiples. Le 14e degrés s'assimile à une octave bien qu'elle soit plus haute de 44,44.. cents (1244,44.. cents contre 1200 cents) et le 8e degrés s'assimile à la quinte bien qu'elle sonne plus haut de 11,11.. cents (711,11.. cents contre 700 cents). 12,5 cents correspond à l'intervalle de 1/16e de ton.

cycle : 6te m
nbr de degrés : 9
nom tonal : 4/9e de ton
sensation d'octave : au 14e degré ou au 9+5e degré
valeur dérivée de l'octave : 1244,44.. cents contre 1200 cents

rang -1
...
1° : -88,88.. cents

rang 1
0° : 0 unisson
1° : 88,88.. cents
2° : 177,77.. cents
3° : 266,66.. cents
4° : 355,55.. cents
5° : 444,44.. cents
6° : 533,33.. cents
7° : 622,22.. cents
8° : 711,11.. cents
9° : 800 cents 6te m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

rang 2
1° : 888,889.. cents
2° : 977,77.. cents
3° : 1066,66.. cents
4° : 1155,55.. cents
5° : 1244,44.. cents

2. L'échelle 5/9e de ton (111,11.. cents) divise l'intervalle de 7e mineure (1000 cents) en 9 intervalles équidistants et reproduit les intervalles de Z12 tels que : septième mineur, octave + 6e mineur (2 x 7e m), etc. : 5/9e de ton est une échelle cyclique qui répète l'intervalle de 7e m et ses multiples. Le 11e degrés s'assimile à une octave bien qu'elle soit plus haute de 22,22.. cents (1222,22.. cents contre 1200 cents).

cycle : 7e m
nbr de degrés : 9
nom tonal : 5/9e de ton
sensation d'octave au 11e degré ou au 9+2e degré
valeur de l'octave dérivé : 1222,22.. cents contre 1200 cents

rang -1
...
1° () : -111,11.. cents

rang 1
0° : 0 unisson
1° : 111,11.. cents
2° : 222,22.. cents
3° : 333,33.. cents
4° : 444,44.. cents
5° : 555,55.. cents
6° : 666,66.. cents
7° : 777,77.. cents
8° : 888,88.. cents
9° : 1000 cents 7e m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

rang 2
1° : 1111,11.. cents
2° : 1222,22.. cents
...

3. L'échelle 7/9e de ton (155,55.. cents) divise l'intervalle d'8ve+2de majeure (1400 cents) en 9 intervalles équidistants et reproduit les intervalles de Z12 tels que : octave + 2de majeure, double octave et tierce majeure (2 x 8ve+2de M), etc. : 7/9e de ton est une échelle cyclique qui répète l'intervalle de 7e m et ses multiples. Le 8e degrés s'assimile à une octave bien qu'elle soit plus haute de 44,44.. cents (1244,44.. cents contre 1200 cents).

cycle : 8ve+2de M
nbr de degrés : 9
nom tonal : 7/9e de ton
sensation d'octave au 8e degré
valeur de l'octave dérivé : 1244,44.. cents contre 1200 cents

...
rang -1
1° : -155,55.. cents

rang 1
0° : 0 unisson
1° : 155,55.. cents
2° : 311,11.. cents
3° : 466,66.. cents
4° : 622,22.. cents
5° : 777,77.. cents
6° : 933,33.. cents
7° : 1088,88.. cents
8° : 1244,44.. cents
9° : 1400 cents 8ve + 2de M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

rang 2
1° : 1555,55.. cents
2° : 1711,11.. cents
...

4. L'échelle 8/9e de ton (177,77.. cents) divise l'intervalle d'8ve+3ce majeure (1600 cents) en 9 intervalles équidistants et reproduit les intervalles de Z12 tels que : octave + 3ce majeure, double octave et sixte mineure (2 x 8ve+3ce M), etc. : 8/9e de ton est une échelle cyclique qui répète l'intervalle d'8ve+3ce M et ses multiples. Le 7e degrés s'assimile à une octave bien qu'elle soit plus haute de 44,44.. cents (1244,44.. cents contre 1200 cents).

cycle : 8ve+3ce M
nbr de degrés : 9
nom tonal : 8/9e de ton
sensation d'octave au 7e degré
valeur de l'octave dérivé : 1244,44.. cents contre 1200 cents

...
rang -1
1° : -177,77.. cents

rang 1
0° : 0
1°: 177,77.. cents
2° : 355,55.. cents
3° : 533,33.. cents
4° : 711,11.. cents
5° : 888,88.. cents
6° : 1066,66.. cents
7° : 1244,44.. cents
8° (: 1422,22.. cents
9°: 1600 cents 8ve+3ce M
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

rang 2
1° : 1877,77.. cents
2° : 1955,55.. cents
...

5. L'échelle 10/9e de ton (222,22.. cents) divise l'intervalle d'8ve+6te mineure (2000 cents) en 9 intervalles équidistants et reproduit les intervalles de Z12 tels que : octave + 6te mineure, triple octave et tierce majeure (3 x 8ve+6te m), etc. : 10/9e de ton est une échelle cyclique qui répète l'intervalle d'8ve+6te m et ses multiples.

cycle : 8ve+6te m
nbr de degrés : 9
nom tonal : 10/9e de ton
sensation d'octave : néant
valeur de l'octave dérivé : néant

...
rang -1
1° : -222,22.. cents

rang 1
0° : 0 unison
1° : 222,22.. cents
2° : 444,44.. cents
3° : 666,66.. cents
4° : 888,88.. cents
5° : 1111,11.. cents
6° : 1333,33.. cents
7° : 1555,55.. cents
8° : 1777,77.. cents
9° : 2000 cents 8ve+6te m
téléchargez le Scala tuning script .scl. download the tuning script for Kontakt sampler .nkp

rang 2
1° : 2222,22.. cents
2° : 2444,44.. cents
...

...

Suite de presque toutes les échelles nonoctaviantes par ordre de grandeur
multiples de 1/16e, 1/15e, 1/14e, 1/13e, 1/12e, 1/11e, 1/10e et 1/9e de ton

micro-intervalles (+ petit que le 1/2 ton)

n° fractions de ton intervalles cycles repères télécharger télécharger

e1 4/15e de ton = 53,33.. cents divise 800 cents en 15 ~ 23 div ~ 8ve Scala tuning script .scl Kontakt tuning script.nkp

e2 4/13e de ton = 61,53... cents divise 800 cents en 13 ~ 20 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e3 5/16e de ton = 62,5 cents divise 1000 cents en 16, 500 en 8, 250 en 4, 125 en 2 ~ 19 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e4 5/14e de ton = 71,42... cents divise 1000 cents en 14, 500 en 7 ~ 17 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e5 4/11e de ton = 72,72.. cents divise 800 cents en 11 ~ 17 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e6 5/13e de ton = 76,92... cents divise 1000 cents en 13 ~ 16 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e7 5/12e de ton = 83,33.. cents divise 1000 cents en 12, 500 en 6, 250 en 3 ~ 14 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e8 7/16e de ton = 87,5 cents divise 1400 cents en 16, 700 en 8, 350 en 4, 175 en 2 ~ 14 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e9 4/9e de ton = 88,88.. cents divise 800 cents en 9 ~ 14 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e10 5/11e de ton = 90,90.. cents divise 1000 cents en 11 ~ 13 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e11 7/15e de ton = 93,33.. cents divise 1400 cents en 15 ~ 13 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

macro-intervalles (+ grand que le 1/2 ton)

e12 8/15e de ton = 106,66.. cents divise 1600 cents en 15 ~ 11 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e13 7/13e de ton = 107,69... cents divise 1400 cents en 13 ~ 11 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e14 5/9e de ton = 111,11.. cents divise 1000 cents en 9 ~ 11 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e15 9/16e de ton = 112,5 cents divise 1800 cents en 16, 900 en 8 ~ 11 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e16 4/7e de ton = 114,28... cents divise 800 cents en 7 ~ 11 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e17 7/12e de ton = 116,66.. cents divise 1400 cents en 12, 700 en 6 (se résout à la 5te) ~ 10 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e18 8/13e de ton = 123,07... cents divise 1600 cents en 13 ~ 10 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e19 5/8e de ton = 125 cents divise 1000 cents en 8, 500 en 4 (se résout à la 4te) ~ 10 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e20 7/11e de ton = 127,27.. cents divise 1400 cents en 11 (509,09.. cents comme une 4te) ~ 10 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e21 9/14e de ton = 128,57... cents divise 1800 cents en 14, 900 en 7 ~ 10 div ~ no 8ve Scala tuning script .scl Kontakt tuning script .nkp

e22 11/16e de ton = 137,5 cents divise 2200 cents en 16, 1100 en 8 ~ 9 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e23 9/13e de ton = 138,46... cents divise 1800 cents en 13 ~ 9 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e24 7/10e de ton = 140 cents divise 1400 cents en 10, 700 en 5 ~ 9 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e25 5/7e de ton = 142,85... cents divise 1000 cents en 7 ~ 9 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e26 8/11e de ton = 145,45.. cents divise 1600 cents en 11 ~ 8 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e27 11/15e de ton = 146,66.. cents divise 2200 cents en 15 ~ 8 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e28 10/13e de ton = 153,84... cents divise 2000 cents en 13 ~ 8 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e29 7/9e de ton = 155,55.. cents divise 1400 cents en 9 ~ 8 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e30 11/14e de ton = 157,14... cents divise 2200 cents en 14, 1100 en 7 ~ 8 div ~ no 8ve Scala tuning script .scl Kontakt tuning script .nkp

e31 4/5e de ton = 160 cents divise 800 cents en 5 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e32 13/16e de ton = 162,5 cents divise 2600 cents en 16, 1300 en 8 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e33 9/11e de ton = 163,63.. cents divise 1800 cents en 11 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e34 10/12e de ton = 166,66.. cents divise 2000 cents en 12, 1000 en 6, 500 en 3 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e35 11/13e de ton = 169,23... cents divise 2200 cents en 13 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e36 13/15e de ton = 173,33.. cents divise 2600 cents en 15 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e37 7/8e de ton = 175 cents divise 1400 cents en 8, 700 en 4 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e38 8/9e de ton = 177,77.. cents divise 1600 cents en 9 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e39 9/10e de ton = 180 cents divise 1800 cents en 10, 900 en 5 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e40 10/11e de ton = 181,81.. cents divise 2000 cents en 11 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e41 11/12e de ton = 183,33.. cents divise 2200 cents en 12 ~ 7 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e42 12/13e de ton = 184,61... cents divise 2400 cents en 13 (dbl 8ve div par 13) ~ 7 div ~ no 8ve Scala tuning script .scl Kontakt tuning script .nkp

e43 13/14e de ton = 185,71... cents divise 2600 cents en 14, 1300 en 7 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e44 14/15e de ton = 186,66.. cents divise 2800 cents en 15 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e45 15/16e de ton = 187,5 cents divise 3000 cents en 16, 1500 en 8 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

1ers intervalles + grand que le ton

e46 17/16e de ton = 212,5 cents divise 3400 cents en 16, 1700 en 8, 850 en 4, 425 en 2 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e47 16/15e de ton = 213,33.. cents divise 3200 cents en 15 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e48 15/14e de ton = 214,28... cents divise 3000 cents en 14 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e49 14/13e de ton = 215,38... cents divise 2800 cents en 13 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e50 13/12e de ton = 216,66.. cents divise 2600 cents en 12, 1300 en 6 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e51 12/11e de ton = 218,18.. cents divise 2400 cents en 11 (dbl 8ve div par 11) ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e52 11/10e de ton = 220 cents divise 2200 cents en 10, 1100 en 5 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

e53 10/9e de ton = 222,22.. cents divise 2000 cents en 9 ~ 6 div ~ 8ve Scala tuning script .scl Kontakt tuning script .nkp

Téléchargez les 53 échelles nonoctaviantes (au format Scala .scl in .zip 21Ko)
Téléchargez les 53 échelles nonoctaviantes (au format Kontakt 2 .nkp in .zip 90Ko)
Abaque (mis à jour) des 53 échelles nonoctaviantes tonales [pdf241Ko]

remarque : pour se familiariser avec ces 53 échelles non-octaviantes, on conseille dans un premier temps d'utiliser un instrument de musique familier.
Pianoteq lit directement les fichiers Scala .scl avec des sons de claviers classiques modélisés. Le sampler conteneur Kontakt accepte tous les sons.
svp, s'il y a, rapportez les erreurs

53 ECHELLES NONOCTAVIANTES ISSUES DE :

9 échelles non-octaviantes multiples de 1/16e de ton

Echelle de 5/16e de ton = 62,5 cents
Echelle de 7/16e de ton = 87,5 cents
Echelle de 9/16e de ton = 112,5 cents
Echelle de 5/8e de ton = 125 cents
Echelle de 11/16e de ton = 137,5 cents
Echelle de 13/16e de ton = 162,5 cents
Echelle de 7/8e de ton = 175 cents
Echelle de 15/16e de ton = 187,5 cents
Echelle de 17/16e de ton = 212,5 cents

8 échelles non-octaviantes multiples de 1/15e de ton

Echelle de 4/15e de ton = 53,33.. cents
Echelle de 7/15e de ton = 93,33.. cents
Echelle de 8/15e de ton = 106,66.. cents
Echelle de 11/15e de ton = 146,66.. cents
Echelle de 4/5e de ton = 160 cents
Echelle de 13/15e de ton = 173,33.. cents
Echelle de 14/15e de ton = 186,66.. cents
Echelle de 16/15e de ton = 213,33.. cents

7 échelles non-octaviantes multiples de 1/14e de ton

Echelle de 5/14e de ton = 71,42... cents
Echelle de 4/7e de ton = 114,28... cents
Echelle de 9/14e de ton = 128,57... cents
Echelle de 5/7e de ton = 142,85... cents
Echelle de 11/14e de ton = 157,14... cents
Echelle de 13/14e de ton = 185,71... cents
Echelle de 15/14e de ton = 214,28... cents

9 échelles non-octaviantes multiples de 1/13e de ton

Echelle de 4/13e de ton = 61,53... cents
Echelle de 5/13e de ton = 76,92... cents
Echelle de 7/13e de ton = 107,69... cents
Echelle de 8/13e de ton = 123,07... cents
Echelle de 9/13e de ton = 138,46... cents
Echelle de 10/13e de ton = 153,84... cents
Echelle de 11/13e de ton = 169,23... cents
Echelle de 12/13e de ton = 184,61... cents (dbl oct div par 13)
Echelle de 14/13e de ton = 215,38... cents

5 échelles non-octaviantes multiples de 1/12e de ton

Echelle de 5/12e de ton = 83,33.. cents
Echelle de 7/12e de ton = 116,66.. cents
Echelle de 10/12e de ton = 166,66.. cents
Echelle de 11/12e de ton = 183,33.. cents
Echelle de 13/12e de ton = 216,66.. cents

7 échelles non-octaviantes multiples de 1/11e de ton

Echelle de 4/11e de ton = 54,54.. cents
Echelle de 5/11e de ton = 90,90.. cents
Echelle de 7/11e de ton = 127,27.. cents
Echelle de 8/11e de ton = 145,45.. cents
Echelle de 9/11e de ton = 163,63.. cents
Echelle de 10/11e de ton = 181,81.. cents
Echelle de 12/11e de ton = 218,18.. cents (dbl oct div par 11)

3 échelles non-octaviantes multiples de 1/10e de ton

Echelle de 7/10e de ton = 140 cents
Echelle de 9/10e de ton = 180 cents
Echelle de 11/10e de ton = 220 cents

5 échelles non-octaviantes multiples de 1/9e de ton

Echelle de 4/9e de ton = 88,88.. cents
Echelle de 5/9e de ton = 111,11.. cents
Echelle de 7/9e de ton = 155,55.. cents
Echelle de 8/9e de ton = 177,77.. cents
Echelle de 10/9e de ton = 222,22.. cents (double de 5/9e de ton)

Remarques
. Les micro-intervalles non-octaviants se situent entre le quart de ton (50 cents) et le demi-ton (100 cents), calculés à partir de l'échelle de 1/16e de ton. Pour affiner au-delà du 1/4 de ton, il faut descendre encore plus bas que le 1/16e de ton.
. Il y a + de macroéchelles non-octaviantes que de microéchelles non-octaviantes : 34 macroéchelles pour 11 microéchelles.
. Nous nous sommes arrêtés juste après le ton (200 cents).
. Il existe 53 échelles non-octaviantes calculées à partir du 1/16e de ton (12,5 cents) jusqu'au premier intervalle après le ton (200 cents).
. Il existe 2 échelles doubles octaviantes : l'échelle de 12/13e de ton (184,6153... cents) et celle de 12/11e de ton (218,18.. cents), aussi la largeur des intervalles empêche l'existence d'une note sensible qui oblige à l'octaviation, à la résolution dans l'octave bien qu'elles restent double-octaviantes.
. Il existe 51 échelles non-octaviantes calculées à partir du 1/16e de ton (12,5 cents) jusqu'au premier intervalle après le ton (200 cents).
. L'ambitus divisé des échelles non-octaviantes est toujours un intervalle appartenant à Z12 : 800 (6te m), 1000 (7e m) et 1400 (8ve + 2d M) pour les échelles microintervallaires puis 800 (6te m), 1000 (7e m), 1400 (8ve + 2d M), 1600 (8ve + 3ce M), 1800 (8ve + 4te+), 2000 (8ve + 6te m), 2200 (8ve + 7e m), 2400 (dbl 8ve), 2600 (dbl 8ve + 2de M), 3000 (dbl 8ve + 4te+) pour les échelles macrointervallaires. Ces ambitus non-octaviants forment des cycles appartenant à Z6 qui est la "gamme par ton de Debussy" puisque le ton est l'intervalle référant et divisé pour obtenir ces échelles non-octaviantes avec les échelles de : 1/16e de ton, 1/15e de ton, 1/14e de ton, 1/13e de ton, 1/12e de ton, 1/11e de ton, 1/10e de ton et 1/9e de ton.
. L'échelle de 7/12e de ton (116,66.. cents) se résout dans la quinte : le 6e et le 2d degrés sont sensibles.
. L'échelle de 5/8e de ton (125 cents) se résout dans la quarte : le 4e et 2d degrés sont sensibles.

Identification des cycles et de leurs "stries"
les cycles divisés sont des intervalles éléments de Z12
il y a 19 familles cyclées nonoctaviantes

. Il y a
5
échelles nonoctaviantes qui divisent le cycle de la quarte (4te = 500 cents) en 8, 7, 6, 4 et 3 (div. paires+impaires) 5/16e de ton, 5/14e de ton, 5/12e de ton, 5/8e de ton et 10/12e de ton

. Il y a
0
échelle nonoctaviante qui divise le cycle de la quarte augmentée (4te+ = 600 cents)

. Il y a
4
échelles nonoctaviantes qui divisent le cycle de la quinte (5te = 700 cents) en 8, 6, 5, et 4 (div. paires+impaire) 7/16e de ton, 7/12e de ton, 7/10e de ton et 7/8e de ton

. Il y a
6
échelles nonoctaviantes qui divisent le cycle de la sixte mineure (6te m = 800 cents) en 15, 13, 11, 9, 7 et 5 (div. impaires)

. Il y a
3
échelles nonoctaviantes qui divisent le cycle de la sixte majeure (6te M = 900 cents) en 8, 7 et 5 (div. paire+impaires)

. Il y a
4
échelles nonoctaviantes qui divisent le cycle de la septième mineure (7e m = 1000 cents) en 13, 11, 9 et 7 (div. impaires)

. Il y a
3
échelles nonoctaviantes qui divisent le cycle de la septième majeure (7e M 1100 cents) en 8, 7 et 5 (div. paire+impaires)

. Il y a
3
échelles nonoctaviantes qui divisent le cycle de l'octave et seconde mineure (8ve+2de m = 1300 cents) en 8, 7 et 6 (div. paires+impaire)

. Il y a
3
échelles nonoctaviantes qui divisent le cycle de l'octave et seconde majeure (8ve+2de M = 1400 cents) en 15, 13 et 9 (div. impaires)

. Il y a
1
échelle nonoctaviante qui divise le cycle de l'octave et tierce mineure (8ve+3ce m = 1500 cents) en 8 (div. paire)

. Il y a
4
échelles nonoctaviantes qui divisent le cycle de l'octave et tierce majeure (8ve+3ce M = 1600 cents) en 15, 13, 11 et 9 (div. impaires)

. Il y a
1
échelle nonoctaviante qui divise le cycle de l'octave et quarte (8ve+4te = 1700 cents ) en 8 (div. paire)

. Il y a
2
échelles nonoctaviantes qui divisent le cycle de l'octave et quarte augmentée (8ve+4te+ = 1800 cents) en 13 et 11 (div. impaires)

. Il y a
0
échelle nonoctaviante qui divise le cycle de l'octave et quinte (8ve+5te = 1900 cents)

. Il y a
3
échelles nonoctaviantes qui divisent le cycle de l'octave et sixte mineure (8ve+6te m = 2000 cents) en 13, 11 et 9 (div. impaires)

. Il y a
0
échelle nonoctaviante qui divise le cycle de l'octave et sixte majeure (8ve+6te M = 2100 cents)

. Il y a
3
échelles nonoctaviantes qui divisent le cycle de l'octave et septième mineure (8ve+7e m = 2200 cents) en 15, 13 et 12 (div. impaires+paire)

. Il y a
0
échelle nonoctaviante qui divise le cycle de l'octave et septième majeure (8ve+7e M = 2300 cents)

. Il y a
2
échelles nonoctaviantes qui divisent le cycle de double octave (2.8ve = 2400 cents) en 13 et 11 (div. impaires)

. Il y a
0
échelle nonoctaviante qui divise le cycle de double octave et seconde mineure (2.8ve+2de m = 2500 cents)

. Il y a
1
échelle nonoctaviante qui divise le cycle de double octave et seconde majeure (2.8ve+2de M = 2600 cents) en 15 (div. impaire)

. Il y a
0
échelle nonoctaviante qui divise le cycle de double octave et tierce mineure (2.8ve+3ce m = 2700 cents)

. Il y a
2
échelles nonoctaviantes qui divisent le cycle de double octave et tierce majeure (2.8ve+3ce M = 2800 cents) en 15 et 13 (div. impaires)

. Il y a
0
échelle nonoctaviante qui divise le cycle de double octave et quarte (2.8ve+4te = 2900 cents)

. Il y a
1
échelle nonoctaviante qui divise le cycle de double octave et quarte augmentée (2.8ve+4te+ = 3000 cents) en 14 (div. paire)

. Il y a
0
échelle nonoctaviante qui divise le cycle de double octave et quinte (2.8ve+5te = 3100 cents)

. Il y a
1
échelle nonoctaviante qui divise le cycle de double octave et sixte mineure (2.8ve+6te m = 3200 cents) en 15 (div. impaire)

Remarques
. Il y a 19 cycles d'intervalles de Z12 qui offrent 53 échelles non-octaviantes.
. Il y a 11 types de divisions dont 4 divisions paires : 4, 6, 8 et 12 (une fois) et 7 divisions impaires : 3, 5, 7, 9, 11, 13 et 15 dont 5 sont premières (= des nombres premiers. 6 est à la fois paire et impaire et nous aurions pû le placer dans la famille impaire) qui divisent les 19 cycles.
. Pas de division en dessous de l'ambitus de quarte = 500 cents.
. Les échelles qui retrouvent la quinte (5te) et la quarte (4te) dans un cycle, sont les échelles multiplent d'1/16e de ton, d'1/14e de ton, d'1/12e de ton et d'1/10e de ton : toutes les quatres à division paire.
. 6 cycles rassemblent à la fois des divisions paires et impaires. Le cycle de l'octave et septième mineure (8ve+7e m = 2200 cents) rassemble à la fois des divisions impaires et paire : 15, 13 et 12, mais est le seul à avoir une division par 12 dans le groupe.
. 10 cycles ont des divisions impaires.
. 3 cycles ont des divisions paires et uniques : 8, 8, 14.

Va-t-on vérifier les autres divisions de ces cycles ? Oui.
...

Rappel :

notes do do# ré ré# mi fa fa# sol sol# la la# si do

cents 0 100 200 300 400 500 600 700 800 900 1000 1100 1200

intervalles unisson 2de m 2de M 3ce m 3ce M 4te 4te+ 5te 6te m 6te M 7e m 7e M 8ve

Téléchargez toutes les 53 échelles non-octaviantes (au format Scala .scl in .zip 21Ko)
Téléchargez toutes les 53 échelles non-octaviantes (au format Kontakt 2 .nkp in .zip 90Ko)
Pour tout autre instrument prendre le format Scala .scl et l'exporter au format accépté de l'instrument avec une exportation à partir de Scala même (avec la commande "send").
Téléchargez l'abaque des 53 échelles nonoctaviantes (format A3 pdf 41Ko)
Téléchargez la mise à jour de l'abaque des 53 échelles nonoctaviantes [A3 pdf 241Ko]
Download the Mathius Shadow-Sky 53 nonoctave scales chart (A3 pdf format 41Ko)
Download the Mathius Shadow-Sky 53 nonoctave scales updated chart [A3 pdf 241Ko]

et... ?

A quoi peut servir l'usage d'autres échelles de divisions égales divisant des nonoctaves ?
et d'en avoir plusieurs du même type ?

est-ce une histoire de « regroupement familial » ou tribal ?

Dans les 53 échelles nonoctaviantes découvertes, nous avons une série de nonoctaves proche d'octave non multiples de 2 (1200 cents) telles que :

n° nonoctaves
divisions nonoctaviantes
composition des familles

e1 1226,66.. cents
23
famille 23 : 1 enfant

e2 1230,769230...... cents
20
famille 20 : 1 enfant

e3 1187,5 cents
19
famille 19 : 1 enfant

e4 1214,285714...... cents
17
famille 17 : 2 enfants

e5 1236,36.. cents

e6 1230,769230...... cents
16
famille 16 : 1 enfant

e7 1166,66.. cents
14 (ou 1250 cents pour div. 15)
famille 14 : 3 enfants (ou famille 14 : 2 enfants et famille 15 : 1 enfant qui se partage 2 familles)

e8 1225 cents
14

e9 1244,44.. cents

e10 1181,81.. cents
13
famille 13 : 2 enfants

e11 1213,33.. cents

frontière micro et macro intervalles

e12 1173,33.. cents
11
famille 11 : 5 enfants

e13 1184,615384...... cents

e14 1222,22.. cents

e15 1237,5 cents

e16 1257,142857...... cents

e17 1166,66.. cents
10
famille 10 : 3+2 enfants avec 2 enfants qui se partagent avec la famille 9

e18 1230,769230...... cents

e19 1250 cents

e20 1272,72.. cents
10 (ou 1145,45.. cents pour div. par 9)

e21 1285,714285...... cents
10 (ou 1157,142857...... pour div. par 9)

e22 1237,5 cents
9
famille 9 : 4+2 enfants avec 2 enfants qui se partagent avec la famille 10

e23 138,461538...... (?) cents

e24 1260 cents

e25 1142,857142...... cents

e26 1163,63.. cents
8
famille 8 : 4+1 enfants avec 1 enfant qui se partage avec la famille 7

e27 1173,33.. cents

e28 1230,769230...... cents

e29 1244,44.. cents

e30 1257,142857...... cents
8 (ou 1100 cents pour div. par 7)

e31 1120 cents
7
famille 7 : 11+1 enfants avec 1 enfant qui se partage avec la familles 6

e32 1137,5 cents

e33 1145,45.. cents

e34 1166,66.. cents

e35 1184,615384...... cents

e36 1213,33.. cents

e37 1225 cents

e38 1244,44.. cents

e39 1260 cents

e40 1272,72.. cents

e41 1283,33.. cents

e42 1292,307692...... cents
7 (ou 1107,692307...... cents pour div. par 6)

e43 1114,285714...... cents
6

e44 1120 cents

e45 1125 cents

frontière au-delà du ton

e46 1275 cents
6
famille 6 : 8+4 enfants avec 1 enfant qui se partage avec la famille 7, et 3 enfants qui se partagent avec la famille 5

e47 1280 cents

e48 1285,714285...... cents

e49 1292,307692...... cents

e50 1300 cents

e51 1309,09.. cents
6 (ou 1090,90.. cents pour div. par 5)

e52 1320 cents
6 (ou 1100 cents pour div. par 5)

e53 1333,33.. cents
6 (ou 1111,11.. cents pour div. par 5)

Remarques :
. La tolérance à la sensation d'octave qui dépend du contexte et de chacun : notre « marge perceptive », ne dépasse toujours pas + ou - 12,5 cents (1/16e de ton), ce qui donne soit 8ve+1/16e de ton = 1212,5 cents, soit 8ve-1/16 de ton = 1187,5 cents. Ma sensation d'octave se perd + ou - au-dessus et en dessous. L'octave gouffre à un rapport stricte de 2 et rayonne au-delà de son propre rapport. Ce rayonnement brouillant de l'octaviation (notion de fusion) est dépendant de la perception (l'idée de la fusion) et de la projection (culturelle) de chacun. Mais l'affinement de la perception se travaille à l'usage.
. Le nombre d'échelles nonoctaviantes, ici 53, dépend de la division la plus serrée choisie : ici l'échelle de 1/16e de ton. Il est bien sûr possible de peupler plus les familles en prenant une coupure plus fine. Dans la microtonalité, il existe tellement de subtilités que la macrotonalité saute par bonds.
. Tous les calculs sont à revérifer (il ne le sont pas encore) pour l'ajustement du champ des choses (j'ai une fâcheuse manie à me tromper dans les calculs, une réaction congénitale au systémisme sans doute).

34 nonoctaves en cent (certaines sont communes à plusieurs échelles nonoctaviantes) par ordre croissant des 52 échelles nonoctaviantes (manque e23) :

1114,28... (e43) ;
1120 (e31, e44) ;
1125 (e45) ;
1137,5 (e32) ;
1142,85... (e25) ;
1145,45.. (e33) ;
1163,63.. (e26) ;
1166,66.. (e7, e17, e34) ;
1173,33.. (e12, e27) ;
1181,81.. (e10) ;
1184,61... (e13, e35) ;
1187,5 (e3) ;

1213,33.. (e11, e36) ;
1214,28... (e4) ;
1222,22.. (e14) ;
1225 (e8, e37) ;
1226,66.. (e1) ;
1230,76... (e2, e6, e18, e28) ;
1236,36.. (e5) ;
1237,5 (e22, e15) ;
1244,44.. (e9, e29, e38) ;
1250 (e19) ;
1257,14... (e16, e30) ;
1260 (e24, e39) ;
1272,72.. (e40, e20) ;
1275 (e46) ;
1280 (e47) ;
1283,33.. (e41) ;
1285,71... (e48, e21) ;
1292,307... (e49, e42) ;
1300 (e50) ;
1309,09.. (e51) ;
1320 (e52) ;
1333,33.. (e53) ;

L'antioctaviation est un procédé qui donne la possibilité de s'échapper du cercle (vicieux ?) de l'attraction binaire. L'antioctaviation permet d'ouvrir des champs inexplorables dans le contexte d'une circulation de l'encerclement sur elle-même. De procéder à l'ouverture du système monoscalaire circulaire tempéré octaviant Z12 sur des champs multiscalaires nonoctaviants (d'échelles cycliques ou noncycliques) et se détacher des attractions obligées. Du poids des choses ? à l'image d'une société libre.

SOMMATION évaluante des échelles divisant le ton (200 cents)

Il y a
46 échelles nonoctaviantes et
54 échelles octaviantes
multiples des 8 tribus d'échelles octaviantes
qui ne dépassent pas l'intervalle de ton (⁶√2 ou 200 cents).

8 _{1/n_e de ton} = {1/16e de ton ; 1/15e de ton ; 1/14e de ton ; 1/13e de ton ; 1/12e de ton ; 1/11e de ton ; 1/10e de ton ; 1/9e de ton}

et .. échelles nonoctaviantes qui ne dépassent pas l'intervalle de ⁵√2 ou 240 cents.

Constat 1 & 2 :

=> Il existe dans toute échelle octaviante au moins une échelle nonoctaviante multiple.

=> Chaque échelle nonoctaviante issue de la division du ton, divise le cycle d'un intervalle de Z12 : 4te, 5te, 6te m, 6te M, 7e m, 7e M, 8ve+2de m, 8ve+2de M, 8ve+3ce m, 8ve+3ce M, 8ve+4te, etc., jusqu'à double 8ve+3ce M (3200 cents).

.

Téléchargements

Téléchargez l'abaque des 53 échelles nonoctaviantes (format A3 pdf 41Ko)
Téléchargez la mise à jour de l'abaque des 53 échelles nonoctaviantes [A3 pdf 241Ko]
Download the Mathius Shadow-Sky 53 nonoctave scales chart (A3 pdf format 41Ko)
Download the Mathius Shadow-Sky 53 nonoctave scales updated chart [A3 pdf 241Ko]

Téléchargez toutes les 53 échelles nonoctaviantes (au format Scala .scl in .zip 21Ko)
Téléchargez toutes les 53 échelles nonoctaviantes (au format Kontakt 2 .nkp in .zip 90Ko)

...

post Note
Le sampler est un instrument qui permet de contenir tout autre instrument, acoustique et électronique (successivement et simultanément). À la fois il rassemble, déclenche et module (contrôleurs MIDI) les échantillons. Son passage en instrument virtuel dans l'ordinateur permet de lire des échantillons à la fois multipistes et aussi longs que le disque dur le permet. Nous avons choisi de travailler avec Kontakt 2, car c'est le seul sampler natif à accepter les scripts que le programme Scala génère. Cependant Kontakt (comme tous les samplers natifs) a une tendance à rendre les sons moins présents une fois chargés et joués dans le sampler, à leur donner un flou qui superposé à d'autres, efface le contour de l'identification (nous avons partiellement résolu le problème en doublant le sample plus une petite cloche EQ maximum de +3dB environ entre 300 et 6kHz suivant le son). Aussi il ne peut comme certains instruments MIDI « hardware » (je pense aux samplers Ensoniq ou Kurzweil) changer d'échelle pendant le jeu en direct de la musique; avec le sysex (system exclusif) ou le MIDI tuning dump*. Pour changer d'échelle avec Kontakt et les autres pendant le jeu, il faut copier le même échantillon sur un autre canal MIDI avec une autre échelle : en changeant de canal, on change d'échelle. Ce sont des avantages contre des inconvénients, des inconvénients contre des avantages. En revanche, nous compositeurs nous devons composer avec ce qui nous est donné (pour les non-programmeurs inventeurs bricoleurs) et cela relève toujours de l'acrobatie à concorder un possible avec une possibilité.

Note de la note
* : presque tous les synthétiseurs Yamaha, du DX7II au VL-7 permettent le MIDI dump, aussi pour le changement d'échelle en temps réel pendant le jeu : mais peu de compositeurs à part quelques « originaux » comme Wendy Carlos (plus adepte du Kurzweil) et d'autres inconnus en ont exploité ces possibilités. Encore aujourd'hui la synthèse par modulation de fréquence** de John Chowning mélangée avec l'utilisation d'échelle autre que celle de 12 tons divisant l'octave*** reste marginale (Yamaha a stoppé la production de synthétiseurs à modulation de fréquence avec le TG77 et le SY99 en 1993 (?)). Tous les synthétiseurs et samplers n'ont pas la capacité de changer leur table d'accord (tuning table) interne. Et les peux de synthétiseurs qui ont une table d'accord variable (par exemple Korg) n'ont pas été construit avec une résolution et des écarts suffisants pour jouer des échelles, modes et gammes de toutes provenances. (the World Music Menu, 1987-2004 par Stephen Nachmanovitch). Reste ceux-ci : Kurzweil K2000, K2500, K2600 and K150 (étonnant que Scala n'est pas compatible avec Kurzweil : le sampler hardware le plus flexible au reaccordage). E-mu Proteus (all models), Morpheus, Ultra Proteus, Proteus 1000, 2000, 2500. Yamaha SY99, SY77, TG77, VL1, TX802, TX81Z, & DX7II. Ensoniq MR-61, MR-76, MR-Rack. Native Instruments FM7, Kontakt 2, Pro-53. Scala en énumère un peu plus (sans les samplers Kurzweil)****.

Note de la note de la note
** certains compositeurs « spectraux » se servent de cette synthèse comme générateur d'accords « non-harmoniques ».
*** avec ses modes usuels : majeur, mineur et pentatonique.
**** L'application « World Music Menu » de Stephen Nachmanovitch (adepte de « l'intonation juste » [pythagoricienne ou plus tôt Chaldéenne de Mésopotamie ou de Ling Lun en Chine] c'est-à-dire des rapports avec des nombres entiers) fut le premier programme informatique (que j'ai connu) proposant une collection de gammes d'accordages différents (du Monde) pour les synthétiseurs et samplers numériques. Sa durée de vie : 1987 - 2004. Stephen Nachmanovitch publie un petit ouvrage « Introduction to Tuning » (http://www.freeplay.com/Writings/Tuning.pdf) qui explique de façon assez claire quelques faits dans la manipulation occidentale des hauteurs dont voici quelques extraits traduits :

« En musique, il n'existe pas d'oreille absolue ou de hauteur absolue. On perçoit toujours une hauteur en rapport et en relation avec un ton fondamental ou un ton référent. » Ce qui est nommée : « oreille absolue », est en fait une excellente mémoire qui reconnait les hauteurs d'une échelle ou d'un mode en fonction du diapason référent de 440Hz pour le la3, ainsi que ses intervalles. (...) « Les gammes, en général, possèdent 5, 7 ou 12 intervalles. » (...) « Une « note » ne représente pas un seul ton, mais toute une région de tons qui sont proches les uns des autres, mais distincts les uns des autres. Les différences de la même note (par exemple do) dépendent du contexte musical de la gamme employée. » (...) « Comme il est difficile de se représenter et de comparer des rapports de nombres entiers (exemple lequel de 64/45 est plus grand ou plus petit que 45/32 ?), le musicologue Alexandre Ellis invente en 1885 le cent, dont 100 cents représente le demi-ton égalisé. Convertir les rapports (x/y) en cents permet une comparaison rapide des différents intervalles. La formule de conversion est : cents = log(ratio)/log(2) x 1200. Ce qui nous donne par exemple pour la quinte harmonique 3/2 une valeur arrondie à 702 cents (701,9550008653874177444867327349... = log [3/2] / log [2] x 1200) au lieu des 700 cents de la 5te égalisée. Ou pour la tierce majeure harmonique de 5/4, 386 cents au lieu de 400 cents de la 3ce majeure égalisée. Dans l'exemple ci-dessus 64/45 correspond à 610 cents et 45/32 correspond à 590 cents contre les 600 cents du triton égalisé. Un système similaire au cent fut développé en Chine, basé sur les puissances de 3. »

Critique
La croyance à « l'intonation juste » provient de l'ancienne querelle entre « consonance » et « dissonance », pensant que des rapports de nombres entiers (entiers naturels éléments de N) permettent la consonance alors que des rapports de nombres non entiers (tels que les nombres réels élément de R) ne le permettent pas (ou provoquent la dissonance). Cette querelle aujourd'hui n'a plus de sens, car depuis plus d'une cinquantaine d'années les musiciens et les compositeurs ont introduit les sons jugés autrefois comme « bruits » dans leur musique (ce qui a permis d'utiliser une pléthore de sonorités inusitées). La notion d'agréable et d'insupportable n'a rien à voir avec la musique et relève plus du domaine de la morale et de la culture : voir dans ce sens notre abaque « musique, son, bruit, agréable, insupportable ». Pour Stephen Nachmanovitch plus les rapports de nombres entiers sont grands plus ils sont dissonants, bien qu'il affirme la beauté de l'intervalle chinois Seven Liü de 729/512 ou arabe Rahawi de 262144/177147. Mathématiquement les rapports d'égalité du périmètre d'un cercle π2 (onde fondamentale) ne se vérifie pas avec ses multiples 2/2, 4/4, 8/8, 16/16, etc. puisque π tendrait vers 2 qui correspond au diamètre du cercle : c'est un paradoxe (Pi = 3,1415926535897932384626433832795...). Ce qui signifie que si deux courbes tendent l'une vers l'autre, elles ne sont pas nécessairement de même longueur. Ce qui nous permet de conclure que le calcul ne rejoint pas nécessairement notre perception et que les notions de juste et de faux (d'injuste) sont aussi relatives que la morale d'une culture de ce qui est acceptable ou pas.

SUITE EXPLORATOIRE :

L'exploration des échelles octaviante tonalisées nous a montré l'existence d'échelles nonoctaviantes au sein même du tempérament octaviant. Pouvait-on s'y attendre ? Ces découvertes nous apprennent que la nonoctaviation existe aussi dans la division d'autres intervalles inclus dans l'octaviation tempérée comme la quarte, la quinte, la sixte mineure, la sixte majeure, la septième mineure et d'autres intervalles plus grands que l'octave. Dans les 53 échelles nonoctaviantes découvertes, 5 divisent la quarte, 4 divisent la quinte, 6 divisent la sixte mineure, 3 divisent la sixte majeure, 4 divisent la septième mineure, 3 divisent la septième majeure, 2 divisent une octave et seconde mineure, etc. En rapport avec tous ces intervalles tonaux divisés, nous allons dénombrer les autres échelles nonoctaviantes qui s'y dissimulent.

...

SUITE EXPLORATOIRE 2

SUITE EXPLORATOIRE 3

SUITE EXPLORATOIRE 4

DES ECHELLES NONOCTAVIANTES

DES CONNEXIONS SCALAIRES

DES TRANSFORMATIONS SCALAIRES

DES MODES NONOCTAVIANTS

DES ACCORDS NONOCTAVIANTS - ET LEURS MUTATIONS
dans l'amas du bruit du silence des armes au nid

.

A la recherche des échelles nonoctaviantes dans la division de l'octave

A la recherche des échelles nonoctaviantes dans la division des nonoctaves éléments de Z12

A la recherche des échelles nonoctaviantes à partir des intervalles de la série harmonique

Les échelles : les suites en séries infinies pour les hôtes ou le savoir scalaire

Comment noter toutes les échelles pour les musiciens ?

L'harmonie nonoctaviante, révolution musicale

Théorie des Champs Scalaires

hauteur
intervalle
échelle
mode

suite

re tour à la table des matières

	nom	rapport				quant. en cent	propriété
1	Echelle de 1/17^e de ton	(2^1/102)¹	=	1,0068	<=>	11,76	symétrique octaviante	= ¹⁰²√2
2	Echelle de 2/17^e de ton	(2^1/102)²	=	1,01368	<=>	23,53	asymétrique octaviante	= ⁵¹√2
3	Echelle de 3/17^e de ton	(2^1/102)³	=	1,0206	<=>	35,29	symétrique octaviante	= ³⁴√2
4	Echelle de 4/17^e de ton	(2^1/96)⁴	=	1,02755	<=>	47,06	asymétrique nonoctaviante
5	Echelle de 5/17^e de ton	(2^1/102)⁵	=	1,03456	<=>	58,82	asymétrique nonoctaviante
6	Echelle de 6/17^e de ton	(2^1/102)⁶	=	1,0416	<=>	70,58	asymétrique octaviante	= ¹⁷√2
7	Echelle de 7/17^e de ton	(2^1/102)⁷	=	1,0487	<=>	82,35	asymétrique nonoctaviante
8	Echelle de 8/17^e de ton	(2^1/102)⁸	=	1,05587	<=>	94,12	asymétrique nooctaviante
9	Echelle de 9/17^e de ton	(2^1/102)⁹	=	1,063	<=>	105,88	asymétrique nonoctaviante
10	Echelle de 10/17^e de ton	(2^1/102)¹⁰	=	1,0703	<=>	117,65	asymétrique nonoctaviante
11	Echelle de 11/17^e de ton	(2^1/102)¹¹	=	1,0776	<=>	129,41	asymétrique nonoctaviante
12	Echelle de 12/17^e de ton	(2^1/102)¹²	=	1,08496	<=>	141,17	asymétrique double octaviante	= ¹⁷√4
13	Echelle de 13/17^e de ton	(2^1/102)¹³	=	1,09236	<=>	152,94	asymétrique nonoctaviante
14	Echelle de 14/17^e de ton	(2^1/102)¹⁴	=	1,0998	<=>	164,7	asymétrique nonoctaviante
15	Echelle de 15/17^e de ton	(2^1/102)¹⁵	=	1,1073	<=>	176,47	asymétrique nonoctaviante
16	Echelle de 16/17^e de ton	(2^1/102)¹⁶	=	1,11486	<=>	188,235	asymétrique nonoctaviante
17	Echelle de ton	(2^1/102)¹⁷	=	,12246	<=>	200	symétrique octaviante	= ⁶√2	1
18	Echelle de 18/17^e de ton	(2^1/102)¹⁸	=	1,13	<=>	211,765	asymétrique nonoctaviante
19	Echelle de 19/17^e de ton	(2^1/102)¹⁹	=	1,1378	<=>	223,53	asymétrique triple octaviante	= ¹⁷√8
20	Echelle de 20/17^e de ton	(2^1/102)²⁰	=	1,14558	<=>	235,3	asymétrique nonoctaviante
21	Echelle de 21/17^e de ton	(2^1/102)²¹	=	1,15339	<=>	247,06	asymétrique nonoctaviante

	nom	rapport	en cent
1	Echelle de 4/17^e de ton	1,02755	47,06
2	Echelle de 5/17^e de ton	1,03456	58,82
3	Echelle de 7/17^e de ton	1,0487	82,35
4	Echelle de 8/17^e de ton	1,05587	94,12
5	Echelle de 9/17^e de ton	1,063	105,88
6	Echelle de 10/17^e de ton	1,0703	117,65
7	Echelle de 11/17^e de ton	1,0776	129,41
8	Echelle de 13/17^e de ton	1,09236	152,94
9	Echelle de 14/17^e de ton	1,0998	164,7
10	Echelle de 15/17^e de ton	1,1073	176,47
11	Echelle de 16/17^e de ton	1,11486	188,235
12	Echelle de 18/17^e de ton	1,13	211,765
13	Echelle de 19/17^e de ton	1,1378	223,53
14	Echelle de 20/17^e de ton	1,14558	235,3
15	Echelle de 21/17^e de ton	1,15339	247,06

nom		quantification en cent		rapport
5/16^e	de ton	62,5	cents	(⁹⁶√2)⁵ = 1,03678...
7/16^e	de ton	87,5	cents	(⁹⁶√2)⁷ = 1,05187...
9/16^e	de ton	112,5	cents	(⁹⁶√2)⁹ = 1,06717...
5/8^e	de ton	125	cents	(⁹⁶√2)¹⁰ = 1,07491...
11/16^e	de ton	137,5	cents	(⁹⁶√2)¹¹ = 1,0827...
13/16^e	de ton	162,5	cents	(⁹⁶√2)¹³ = 1,09846...
7/8^e	de ton	175	cents	(⁹⁶√2)¹⁴ = 1,10642...
15/16^e	de ton	187,5	cents	(⁹⁶√2)¹⁵ = 1,11445...
17/16^e	de ton	212,5	cents	(⁹⁶√2)¹⁷ = 1,13066...
9/8^e	de ton	225	cents	(⁹⁶√2)¹⁸ = 1,13886...
19/16^e	de ton	237,5	cents	(⁹⁶√2)¹⁹ = 1,14712...

rang	nom en ton		ambitus tonal (intervalle) divisé			divisant par	nonoctaviation	intervalle en cents	nombre de degrés par 8ve	désignation par densité
1	5/16^e	de ton	500	cents	4te	8	au 19e degré : 1187,5 contre 1200 cents	62,5	19,2	nanodécatonique nonoctaviante
2	7/16^e	de ton	700	cents	5te	8	au 14e degré : 1225 contre 1200 cents	87,5	13,714...	tetradécatonique nonoctaviante
3	9/16^e	de ton	900	cents	6te M	8	au 11e degré : 1237,5 contre 1200 cents	112	10,714...	hendécatonique nonoctaviante
4	5/8^e	de ton	500	cents	4te	4	au 10e degré : 1250 contre 1200 cents	125	9,6	décatonique nonoctaviante
5	11/16^e	de ton	1100	cents	7e M	8	au 9e degré : 1237,5 contre 1200 cents	137,5	8,72..	nonatonique nonoctaviante
6	13/16^e	de ton	1300	cents	8ve+2de m	8	au 7e degré : 1137,5 contre 1200 cents	162,5	7,384...	heptatonique nonoctaviante
7	7/8^e	de ton	700	cents	5te	4	au 7e degré : 1225 contre 1200 cents	175	6,857...	heptatonique nonoctaviante
8	15/16^e	de ton	1500	cents	8ve+3ce m	8	au 6e degré : 1125 contre 1200 cents	187,5	6,4	hexatonique nonoctaviante
9	17/16^e	de ton	1700	cents	8ve+4te	8	au 5e degré : 1275 contre 1200 cents	212,5	5,647...	hexatonique nonoctaviante
10	9/8^e	de ton	900	cents	6te M	4	au 4e degré : 1125 contre 1200 cents	225	5,33..	pentatonique nonoctaviante
11	19/16^e	de ton	1900	cents	8ve+5te	8	au 5e degré : 1187,5 contre 1200 cents	237,5	5,0526...	pentatonique nonoctaviante

	nom	rapport			propriété
1	Echelle de 1/15^e de ton	(2^1/90)¹	=	1,00773	symétrique octaviante	= ⁹⁰√2
2	Echelle de 2/15^e de ton	(2^1/90)²	=	1,01552	asymétrique octaviante	= ⁴⁵√2
3	Echelle de 1/5^e de ton	(2^1/90)³	=	1,02337	symétrique octaviante	= ³⁰√2
4	Echelle de 4/15^e de ton	(2^1/90)⁴	=	1,031286	asymétrique nonoctaviante
5	Echelle de 1/3 de ton	(2^1/90)⁵	=	1,03926	symétrique octaviante	= ¹⁸√2
6	Echelle de 2/5^e de ton	(2^1/90)⁶	=	1,04729	asymétrique octaviante	= ¹⁵√2
7	Echelle de 7/15^e de ton	(2^1/90)⁷	=	1,05539	asymétrique nonoctaviante
8	Echelle de 8/15^e de ton	(2^1/90)⁸	=	1,06355	asymétrique nonoctaviante
9	Echelle de 3/5^e de ton	(2^1/90)⁹	=	1,07177	symétrique octaviante	= ¹⁰√2
10	Echelle de 10/15^e de ton	(2^1/90)¹⁰	=	1,08006	asymétrique octaviante	= ⁹√2
11	Echelle de 11/15^e de ton	(2^1/90)¹¹	=	1,08841	asymétrique nonoctaviante
12	Echelle de 4/5^e de ton	(2^1/90)¹²	=	1,09825	asymétrique nonoctaviante
13	Echelle de 13/15^e de ton	(2^1/90)¹³	=	1,1053	asymétrique nonoctaviante
14	Echelle de 14/15^e de ton	(2^1/90)¹⁴	=	1,11385	asymétrique nonoctaviante
15	Echelle de ton	(2^1/90)¹⁵	=	1,12246	symétrique octaviante	= ⁶√2
16	Echelle de 16/15^e de ton	(2^1/90)¹⁶	=	1,13114	asymétrique non-octaviante
17	Echelle de 17/15^e de ton	(2^1/90)¹⁷	=	1,13988	asymétrique non-octaviante
18	Echelle de 6/5^e de ton	(2^1/90)¹⁸	=	1,148698	asymétrique octaviante	= ⁵√2

nom		quantification en cent		rapport	(rappel : ¹²√2 = 1,05946)
4/15^e	de ton	53,33..	cents	(⁹⁰√2)⁴ = 1,03128...
7/15^e	de ton	93,33..	cents	(⁹⁰√2)⁷ = 1,05538...
8/15^e	de ton	106,66..	cents	(⁹⁰√2)⁸ = 1,06354...
11/15^e	de ton	146,66..	cents	(⁹⁰√2)¹¹ = 1,08839...
4/5^e	de ton	160	cents	(⁹⁰√2)¹² = 1,09681...
13/15^e	de ton	173,33..	cents	(⁹⁰√2)¹³ = 1,10529...
14/15^e	de ton	186,66..	cents	(⁹⁰√2)¹⁴ = 1,11383...
16/15^e	de ton	213,33..	cents	(⁹⁰√2)¹⁶ = 1,13114...
17/15^e	de ton	226,66..	cents	(⁹⁰√2)¹⁷ = 1,13988...

rang	nom en ton		ambitus (intervalle) divisé			divisant par	nonoctave proche octave au	intervalle en cents	nombre de degrés par 8ve	désignation par densité
1	4/15^e	de ton	800	cents	6te m	15	22e degré : 1173 contre 1200	53,33 cents	22,5 (45 degrés pour dbl 8ve)	cycle de 22 tons
2	7/15^e	de ton	1400	cents	8ve+2de M	15	13e degré : 1213 contre 1200 cents	93,33 cents	12,85...	tridécatonique
3	8/15^e	de ton	1600	cents	8ve+3ce M	15	11e degré : 1173 contre 1200 cents	106,66 cents	11,25	hendécatonique
4	11/15^e	de ton	2200	cents	8ve+7e m	15	8e degré : 1173 contre 1200 cents	146,66 cents	8,18..	octotonique
5	4/5^e	de ton	800	cents	6te m	5	15e degré : dbl 8ve 2400 cents	160 cents	7,5 (14 degrés pour dbl 8ve)	tétradécatonique
6	13/15^e	de ton	2600	cents	2x8ve+2de M	15	7e degré : 1213 contre 1200 cents	173,33 cents	6,92...	heptatonique
7	14/15^e	de ton	2800	cents	2x8ve+3ce M	15	6e degré : 1120 contre 1200 cents	186,66 cents	6,42... (quasi dbl 8ve)	hexatonique
8	16/15^e	de ton	3200	cents	2x8ve+6te m	15	17e degré : 3626,66.. contre 3600 cents	213,33 cents	5,62... (quasi trpl 8ve)	heptadécatonique
9	17/15^e	de ton	3400	cents	2x8ve+7e m	15	16e degré : 3626,66.. contre 3600 cents	226,66 cents	5,29... (quasi trpl 8ve)	hexadecatonique

n°	nom		quantification en cent		rapports	exemples musicaux
01	4/15e	de ton	53,33..	cents	1,03128	chopin 4/15	download .scl file
02	5/16e	de ton	62,5	cents	1,03678	chopin 5/16	download .scl file
03	7/16e	de ton	87,5	cents	1,05187	chopin 7/16	download .scl file
04	7/15e	de ton	93,33..	cents	1,05538	chopin 7/15	download .scl file
05	8/15e	de ton	106,66..	cents	1,06354	chopin 8/15	download .scl file
06	9/16e	de ton	112,5	cents	1,06717	chopin 9/16	download .scl file
07	5/8e	de ton	125	cents	1,07491	chopin 5/8	download .scl file
08	11/16e	de ton	137,5	cents	1,0827	chopin 11/16	download .scl file
09	11/15e	de ton	146,66..	cents	1,08839	chopin 11/15	download .scl file
10	4/5e	de ton	160	cents	1,09681	chopin 4/5	download .scl file
11	13/16e	de ton	162,5	cents	1,09846	chopin 13/16	download .scl file
12	13/15e	de ton	173,33..	cents	1,10529	chopin 13/15	download .scl file
13	7/8e	de ton	175	cents	1,10642	chopin 7/8	download .scl file
14	14/15e	de ton	186,66..	cents	1,11383	chopin 14/15	download .scl file
15	15/16e	de ton	187,5	cents	1,11445	chopin 15/16	download .scl file

nom	formule		rapport*		quant. en cents	propriété		remarques
Echelle de 1/14^e de ton	(⁸⁴√2)¹	=	1,00829	<=>	14,2857...	symétrique octaviante	= ⁸⁴√2	1,0082858916953740285765551729555 **
Echelle de 1/7^e de ton	(⁸⁴√2)²	=	1,01665	<=>	28,5714...	symétrique octaviante	= ⁴²√2	1,0166404393919355254466878281669
Echelle de 3/14^e de ton	(⁸⁴√2)³	=	1,02508	<=>	42,8571...	symétrique octaviante	= ²⁸√2	1,0250642119658745674433761912354
Echelle de 2/7^e de ton	(⁸⁴√2)⁴	=	1,03357	<=>	57,1428...	symétrique octaviante	= ²¹√2	1,0335577830070277304532462255542
Echelle de 5/14^e de ton	(⁸⁴√2)⁵	=	1,04214	<=>	71,4285...	asymétrique nonoctaviante		1,0421217308579348537980091159494
Echelle de 3/7^e de ton	(⁸⁴√2)⁶	=	1,05078	<=>	85,7142...	symétrique octaviante	= ¹⁴√2	1,0507566386532194247355350853237
Echelle de 1/2^e de ton	(⁸⁴√2)⁷	=	1,05949	<=>	100 cents	symétrique octaviante	= ¹²√2	= 1,05946 <=> 1/2 ton
Echelle de 4/7^e de ton	(⁸⁴√2)⁸	=	1,06828	<=>	114,2857...	asymétrique nonoctaviante		1,0682416908144022200136068970692
Echelle de 9/14^e de ton	(⁸⁴√2)⁹	=	1,07713	<=>	128,5714...	asymétrique nonoctaviante		1,0770930257689735860738394072839
Echelle de 5/7^e de ton	(⁸⁴√2)¹⁰	=	1,08606	<=>	142,857...	asymétrique nonoctaviante		1,0860177019263380088706088742993
Echelle de 11/14^e de ton	(⁸⁴√2)¹¹	=	1,09507	<=>	157,1428...	asymétrique nonoctaviante		1,09501632698375864013523791702
Echelle de 6/7^e de ton	(⁸⁴√2)¹²	=	1,10414	<=>	171,4285...	symétrique octaviante	= ⁷√2	1,1040895136738123376495053876233
Echelle de 13/14^e de ton	(⁸⁴√2)¹³	=	1,1133	<=>	185,714285...	asymétrique nonoctaviante		1,113237879806111729266212869331
Echelle de ton	(⁸⁴√2)¹⁴	=	1,12253	<=>	200 cents	symétrique octaviante	= ⁶√2	6√2 = 1,12246 ou 1,1224620483093729814335330496792
Echelle de 15/14^e de ton	(⁸⁴√2)¹⁵	=	1,13183	<=>	214,2857...	asymétrique nonoctaviante
Echelle de 8/7^e de ton	(⁸⁴√2)¹⁶	=	1,14121	<=>	228,5714...	asymétrique nonoctaviante
Echelle de 17/14^e de ton	(⁸⁴√2)¹⁷	=	1,15068	<=>	242,8571...	asymétrique nonoctaviante

nom		quantification en cent		rapport
5/14^e	de ton	71,428571428571428571428571428571	cents	(⁸⁴√2)⁵ = 1,04214...
4/7^e	de ton	114,28571428571428571428571428571	cents	(⁸⁴√2)⁸ = 1,06828...
9/14^e	de ton	128,57142857142857142857142857143	cents	(⁸⁴√2)⁹ = 1,07713...
5/7^e	de ton	142,85714285714285714285714285714	cents	(⁸⁴√2)¹⁰ = 1,08606...
11/14^e	de ton	157,14285714285714285714285714286	cents	(⁸⁴√2)¹¹ = 1,09507...
13/14^e	de ton	185,71428571428571428571428571429	cents	(⁸⁴√2)¹³ = 1,1133...
15/14^e	de ton	214,2857...	cents	(⁸⁴√2)¹⁵= 1,13183
8/7^e	de ton	228,5714...	cents	(⁸⁴√2)¹⁶= 1,14121
17/14^e	de ton	242,8571...	cents	(⁸⁴√2)¹⁷= 1,15068

n°	nom		ambitus (intervalle) divisé			division par	nonoctaviation
1	5/14^e	de ton	500	cents	4te	7	au 17e degré : 1214 contre 1200 cents
2	4/7^e	de ton	800	cents	6te m	7
3	9/14^e	de ton	900	cents	6te M	7
4	5/7^e	de ton	1000	cents	7e m	7
5	11/14^e	de ton	1100	cents	7e M	7	Trpl 8ve au 23e degré : 3614 contre 3600 cents
6	13/14^e	de ton	1300	cents	8ve+2de m	7	Dbl 8ve au 13e degré : 2414 contre 2400 cents
7	15/14^e	de ton	1500	cents	8ve+3ce m	7
8	8/7^e	de ton	1600	cents	8ve+3ce M	7
9	17/14^e	de ton	1700	cents	8ve+4te	7

	nom	rapport			propriété
1	Echelle de 1/13^e de ton	(2^1/78)¹	=	1,00892...	symétrique octaviante	= ⁷⁸√2
2	Echelle de 2/13^e de ton	(2^1/78)²	=	1,01793...	asymétrique octaviante	= ⁴⁹√2
3	Echelle de 3/13^e de ton	(2^1/78)³	=	1,02701...	symétrique octaviante	= ²⁶√2
4	Echelle de 4/13^e de ton	(2^1/78)⁴	=	1,03618...	asymétrique nonoctaviante
5	Echelle de 5/13e de ton	(2^1/78)⁵	=	1,04543...	asymétrique nonoctaviante
6	Echelle de 6/13^e de ton	(2^1/78)⁶	=	1,05476...	asymétrique octaviante	= ¹³√2
7	Echelle de 7/13^e de ton	(2^1/78)⁷	=	1,06418...	asymétrique nonoctaviante
8	Echelle de 8/13^e de ton	(2^1/78)⁸	=	1,07368...	asymétrique nonoctaviante
9	Echelle de 9/13^e de ton	(2^1/78)⁹	=	1,08326...	asymétrique nonoctaviante
10	Echelle de 10/13^e de ton	(2^1/78)¹⁰	=	1,09293...	asymétrique nonoctaviante
11	Echelle de 11/13^e de ton	(2^1/78)¹¹	=	1,10268...	asymétrique nonoctaviante
12	Echelle de 12/13e de ton	(2^1/78)¹²	=	1,11253...	asymétrique double-octaviante
13	Echelle de ton	(2^1/78)¹³	=	1,12246...	symétrique octaviante	= ⁶√2
14	Echelle de 14/13^e de ton	(2^1/78)¹⁴	=	1,13248...	asymétrique nonoctaviante
15	Echelle de 15/13^e de ton	(2^1/78)¹⁵	=	1,14258...	asymétrique nonoctaviante
16	Echelle de 16/13^e de ton	(2^1/78)¹⁶	=	1,15278...	asymétrique nonoctaviante
17	Echelle de 17/13^e de ton	(2^1/78)¹⁷	=	1,16307...	asymétrique nonoctaviante
18	Echelle de 18/13^e de ton	(2^1/78)¹⁸	=	1,17346...	asymétrique nonoctaviante

nom		quantification en cent		rapport
4/13^e	de ton	61,5384...	cents	(⁷⁸√2)⁴ = 1,03618...
5/13^e	de ton	76,923...	cents	(⁷⁸√2)⁵ = 1,04543...
7/13^e	de ton	107,6923...	cents	(⁷⁸√2)⁷ = 1,06418...
8/13^e	de ton	123,0769...	cents	(⁷⁸√2)⁸ = 1,07368...
9/13^e	de ton	138,4615...	cents	(⁷⁸√2)⁹ = 1,08326...
10/13^e	de ton	153,846...	cents	(⁷⁸√2)¹⁰ = 1,09293...
11/13^e	de ton	169,2307	cents	(⁷⁸√2)¹¹ = 1,10268...
12/13^e	de ton	184,6153...	cents	(⁷⁸√2)¹² = 1,11253...
et
14/13^e	de ton	215,3846...	cents	(⁷⁸√2)¹⁴ = 1,13248...
15/13^e	de ton	230,76923...	cents	(⁷⁸√2)¹⁵ = 1,14258...
16/13^e	de ton	246,1538...	cents	(⁷⁸√2)¹⁶ = 1,15278...
17/13^e	de ton	261,5384...	cents	(⁷⁸√2)¹⁷ = 1,16307...

rang	5/13e de ton	8ve div 16	différence
01	76,923	75	1,923
02	153,846	150	3,846
03	230,769	225	5,769
04	307,692	300	7,692
05	384,615	375	9,615
06	461,538	450	11,538
07	538,462	525	13,462
08	615,385	600	15,385
09	692,308	675	17,308
10	769,231	750	19,231
11	846,154	825	21,154
12	923,077	900	23,077
13	1000	975	25
14	1076,923	1050	26,923
15	1153,846	1125	28,846
16	1230,769	1200	30,769

rang	20/13e de ton	tierce mineure	différence
01	307,692	300	7,692
02	615,385	600	15,385
03	923,077	900	23,077
04	1230,769	1200	30,769
05	1538,46	1500	38,46
06	1846,152	1800	46,152
07	2153,844	2100	53,844
08	2461,536	2400	61,536

degré	11/13e de ton	mode Majeur	différence
01	169,231	200	30,769
02	338,462	400	61,538
03	507,692	500	7,692
04	676,923	700	23,077
05	846,154	900	53,846
06	1015,385	1100	84,615
07	1184,615	1200	15,385

	nom	rapport			propriété
1	Echelle de 1/12^e de ton	(2^1/72)¹	=	1,00967...	symétrique octaviante	= ⁷²√2
2	Echelle de 1/6^e de ton	(2^1/72)²	=	1,01943...	symétrique octaviante	= ³⁶√2
3	Echelle de 1/4^e de ton	(2^1/72)³	=	1,02929...	symétrique octaviante	= ²⁴√2
4	Echelle de 1/3^e de ton	(2^1/72)⁴	=	1,03924...	symétrique octaviante	= ¹⁸√2
5	Echelle de 5/12e de ton	(2^1/72)⁵	=	1,04929...	asymétrique nonoctaviante
6	Echelle de 1/2 ton	(2^1/72)⁶	=	1,05944...	symétrique octaviante	= ¹²√2
7	Echelle de 7/12^e de ton	(2^1/72)⁷	=	1,06969...	asymétrique nonoctaviante
8	Echelle de 2/3 de ton	(2^1/72)⁸	=	1,08003...	asymétrique octaviante	= ⁹√2
9	Echelle de 3/4 de ton	(2^1/72)⁹	=	1,09047...	symétrique octaviante	= ⁸√2
10	Echelle de 5/6^e de ton	(2^1/72)¹⁰	=	1,10102...	asymétrique nonoctaviante
11	Echelle de 11/12^e de ton	(2^1/72)¹¹	=	1,11167...	asymétrique nonoctaviante
12	Echelle de ton	(2^1/72)¹²	=	1,1224...	symétrique octaviante	= ⁶√2

13	Echelle de 13/12^e de ton	(2^1/72)¹³	=	1,13327...	asymétrique nonoctaviante
14	Echelle de 14/12^e de ton	(2^1/72)¹⁴	=	1,14423...	asymétrique nonoctaviante
15	Echelle de 15/12^e de ton	(2^1/72)¹⁵	=	1,15529...	asymétrique nonoctaviante
16	Echelle de 16/12^e de ton	(2^1/72)¹⁶	=	1,16646...	asymétrique nonoctaviante
17	Echelle de 17/12^e de ton	(2^1/72)¹⁷	=	1,17774...	asymétrique nonoctaviante

nom		quantification en cent		rapport
5/12^e	de ton	83,33..	cents	(⁷²√2)⁵ = 1,04929...
7/12^e	de ton	116,66..	cents	(⁷²√2)⁷ = 1,06969...
5/6^e	de ton	166,66..	cents	(⁷²√2)¹⁰ = 1,10102...
11/12^e	de ton	183,33..	cents	(⁷²√2)¹¹ = 1,11167...
et
13/12^e	de ton	216,66..	cents	(⁷²√2)¹³ = 1,13327...
14/12^e	de ton	233,33..	cents	(⁷²√2)¹⁴ = 1,14423...
15/12^e	de ton	250	cents	(⁷²√2)¹⁵ = 1,15529...
16/12^e	de ton	266,66..	cents	(⁷²√2)¹⁶ = 1,16646...
17/12^e	de ton	283,33..	cents	(⁷²√2)¹⁷ = 1,17774...

	nom	rapport			propriété
1	Echelle de 1/11^e de ton	(2^1/66)¹	=	1,00967...	symétrique octaviante	= ⁶⁶√2
2	Echelle de 2/11^e de ton	(2^1/66)²	=	1,01943...	asymétrique octaviante	= ³³√2
3	Echelle de 3/11^e de ton	(2^1/66)³	=	1,02929...	symétrique octaviante	= ²²√2
4	Echelle de 4/11^e de ton	(2^1/66)⁴	=	1,03924...	asymétrique nonoctaviante
5	Echelle de 5/11^e de ton	(2^1/66)⁵	=	1,04929...	asymétrique nonoctaviante
6	Echelle de 6/11^e de ton	(2^1/66)⁶	=	1,05944...	asymétrique octaviante	= ¹¹√2
7	Echelle de 7/11^e de ton	(2^1/66)⁷	=	1,06969...	asymétrique nonoctaviante
8	Echelle de 8/11^e de ton	(2^1/66)⁸	=	1,08003...	asymétrique nonoctaviante
9	Echelle de 9/11^e de ton	(2^1/66)⁹	=	1,09047...	asymétrique nonoctaviante
10	Echelle de 10/11^e de ton	(2^1/66)¹⁰	=	1,10102...	asymétrique nonoctaviante
11	Echelle de ton	(2^1/66)¹¹	=	1,1224...	symétrique octaviante	= ⁶√2

12	Echelle de 12/11^e de ton	(2^1/66)¹³	=	1,13327...	asymétrique nonoctaviante
13	Echelle de 13/11^e de ton	(2^1/66)¹⁴	=	1,14423...	asymétrique nonoctaviante
14	Echelle de 14/11^e de ton	(2^1/66)¹⁵	=	1,15529...	asymétrique nonoctaviante
15	Echelle de 15/11^e de ton	(2^1/66)¹⁶	=	1,16646...	asymétrique nonoctaviante
16	Echelle de 16/11^e de ton	(2^1/66)¹⁷	=	1,17774...	asymétrique nonoctaviante

nom		quantification en cent		rapport
4/11^e	de ton	72,72..	cents	(⁶⁶√2)⁴ = 1,03924...
5/11^e	de ton	90,90..	cents	(⁶⁶√2)⁵ = 1,04929...
7/11^e	de ton	127,27..	cents	(⁶⁶√2)⁷ = 1,06969...
8/11^e	de ton	145,45..	cents	(⁶⁶√2)⁸ = 1,08003...
9/11^e	de ton	163,63..	cents	(⁶⁶√2)⁹ = 1,09047...
10/11^e	de ton	181,81..	cents	(⁶⁶√2)¹⁰ = 1,1224...
et
13/11^e	de ton	236,36..	cents	(⁶⁶√2)¹³ = 1,13327...
14/11^e	de ton	254,54..	cents	(⁶⁶√2)¹⁴ = 1,14423...
15/11^e	de ton	272,72..	cents	(⁶⁶√2)¹⁵ = 1,15529...
16/11^e	de ton	290,90..	cents	(⁶⁶√2)¹⁶ = 1,16646...
17/11^e	de ton	309,09..	cents	(⁶⁶√2)¹⁷ = 1,17774...

nom		quantification en cent		rapport
7/10^e	de ton	140	cents	(2^1/60)⁷ = 1,08422...
9/10^e	de ton	180	cents	(2^1/60)⁹ = 1,10957...
11/10^e	de ton	220	cents	(2^1/60)¹¹ = 1,135504...

18,181818	1,01055...
36,363636	1,01943...
54,545454	1,02929...
72,727272	1,03924...
90,90909	1,04929...
109,090908	1,05944...
127,272726	1,06969...
145,454544	1,08003...
163,636362	1,09047...
181,81818	1,1224...
200	1,13327...
218,181816	1,13327...
236,363634	1,14423...
254,545452	1,15529...
272,72727	1,16646...
290,909088	1,17774...

	nom	rapport			propriété
1	Echelle de 1/9^e de ton	(2^1/54)¹	=	1,01292...	symétrique octaviante	= ⁵⁴√2
2	Echelle de 2/9^e de ton	(2^1/54)²	=	1,02601...	asymétrique octaviante	= ²⁷√2
3	Echelle de 3/9^e de ton	(2^1/54)³	=	1,03926...	symétrique octaviante	= ¹⁸√2
4	Echelle de 4/9^e de ton	(2^1/54)⁴	=	1,05269...	asymétrique nonoctaviante
5	Echelle de 5/9e de ton	(2^1/54)⁵	=	1,06629...	asymétrique nonoctaviante
6	Echelle de 6/9^e de ton	(2^1/54)⁶	=	1,08007...	asymétrique octaviante	= ⁹√2
7	Echelle de 7/9^e de ton	(2^1/54)⁷	=	1,09402...	asymétrique nonoctaviante
8	Echelle de 8/9^e de ton	(2^1/54)⁸	=	1,10816..	asymétrique nonoctaviante
9	Echelle de ton	(2^1/54)⁹	=	1,1224...	symétrique octaviante	= ⁶√2

10	Echelle de 10/9^e de ton	(2^1/54)¹⁰	=	1,13698...	asymétrique nonoctaviante

11	Echelle de 11/9^e de ton	(2^1/54)¹¹	=	1,15167...	asymétrique nonoctaviante
12	Echelle de 12/9^e de ton	(2^1/54)¹²	=	1,16655...	asymétrique nonoctaviante
13	Echelle de 13/9^e de ton	(2^1/54)¹³	=	1,18162...	asymétrique nonoctaviante
14	Echelle de 14/9^e de ton	(2^1/54)¹⁴	=	1,19688..	asymétrique nonoctaviante
15	Echelle de 15/9^e de ton	(2^1/54)¹⁵	=	1,21235...	asymétrique nonoctaviante
16	Echelle de 16/9^e de ton	(2^1/54)¹⁶	=	1,22801...	asymétrique nonoctaviante

n°	fractions de ton		intervalles	cycles	repères	télécharger	télécharger
e1	4/15e de ton	=	53,33.. cents	divise 800 cents en 15	~ 23 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script.nkp
e2	4/13e de ton	=	61,53... cents	divise 800 cents en 13	~ 20 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e3	5/16e de ton	=	62,5 cents	divise 1000 cents en 16, 500 en 8, 250 en 4, 125 en 2	~ 19 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e4	5/14e de ton	=	71,42... cents	divise 1000 cents en 14, 500 en 7	~ 17 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e5	4/11e de ton	=	72,72.. cents	divise 800 cents en 11	~ 17 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e6	5/13e de ton	=	76,92... cents	divise 1000 cents en 13	~ 16 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e7	5/12e de ton	=	83,33.. cents	divise 1000 cents en 12, 500 en 6, 250 en 3	~ 14 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e8	7/16e de ton	=	87,5 cents	divise 1400 cents en 16, 700 en 8, 350 en 4, 175 en 2	~ 14 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e9	4/9e de ton	=	88,88.. cents	divise 800 cents en 9	~ 14 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e10	5/11e de ton	=	90,90.. cents	divise 1000 cents en 11	~ 13 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e11	7/15e de ton	=	93,33.. cents	divise 1400 cents en 15	~ 13 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp

e12	8/15e de ton	=	106,66.. cents	divise 1600 cents en 15	~ 11 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e13	7/13e de ton	=	107,69... cents	divise 1400 cents en 13	~ 11 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e14	5/9e de ton	=	111,11.. cents	divise 1000 cents en 9	~ 11 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e15	9/16e de ton	=	112,5 cents	divise 1800 cents en 16, 900 en 8	~ 11 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e16	4/7e de ton	=	114,28... cents	divise 800 cents en 7	~ 11 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e17	7/12e de ton	=	116,66.. cents	divise 1400 cents en 12, 700 en 6 (se résout à la 5te)	~ 10 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e18	8/13e de ton	=	123,07... cents	divise 1600 cents en 13	~ 10 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e19	5/8e de ton	=	125 cents	divise 1000 cents en 8, 500 en 4 (se résout à la 4te)	~ 10 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e20	7/11e de ton	=	127,27.. cents	divise 1400 cents en 11 (509,09.. cents comme une 4te)	~ 10 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e21	9/14e de ton	=	128,57... cents	divise 1800 cents en 14, 900 en 7	~ 10 div ~ no 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e22	11/16e de ton	=	137,5 cents	divise 2200 cents en 16, 1100 en 8	~ 9 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e23	9/13e de ton	=	138,46... cents	divise 1800 cents en 13	~ 9 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e24	7/10e de ton	=	140 cents	divise 1400 cents en 10, 700 en 5	~ 9 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e25	5/7e de ton	=	142,85... cents	divise 1000 cents en 7	~ 9 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e26	8/11e de ton	=	145,45.. cents	divise 1600 cents en 11	~ 8 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e27	11/15e de ton	=	146,66.. cents	divise 2200 cents en 15	~ 8 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e28	10/13e de ton	=	153,84... cents	divise 2000 cents en 13	~ 8 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e29	7/9e de ton	=	155,55.. cents	divise 1400 cents en 9	~ 8 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e30	11/14e de ton	=	157,14... cents	divise 2200 cents en 14, 1100 en 7	~ 8 div ~ no 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e31	4/5e de ton	=	160 cents	divise 800 cents en 5	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e32	13/16e de ton	=	162,5 cents	divise 2600 cents en 16, 1300 en 8	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e33	9/11e de ton	=	163,63.. cents	divise 1800 cents en 11	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e34	10/12e de ton	=	166,66.. cents	divise 2000 cents en 12, 1000 en 6, 500 en 3	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e35	11/13e de ton	=	169,23... cents	divise 2200 cents en 13	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e36	13/15e de ton	=	173,33.. cents	divise 2600 cents en 15	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e37	7/8e de ton	=	175 cents	divise 1400 cents en 8, 700 en 4	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e38	8/9e de ton	=	177,77.. cents	divise 1600 cents en 9	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e39	9/10e de ton	=	180 cents	divise 1800 cents en 10, 900 en 5	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e40	10/11e de ton	=	181,81.. cents	divise 2000 cents en 11	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e41	11/12e de ton	=	183,33.. cents	divise 2200 cents en 12	~ 7 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e42	12/13e de ton	=	184,61... cents	divise 2400 cents en 13 (dbl 8ve div par 13)	~ 7 div ~ no 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e43	13/14e de ton	=	185,71... cents	divise 2600 cents en 14, 1300 en 7	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e44	14/15e de ton	=	186,66.. cents	divise 2800 cents en 15	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e45	15/16e de ton	=	187,5 cents	divise 3000 cents en 16, 1500 en 8	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp

e46	17/16e de ton	=	212,5 cents	divise 3400 cents en 16, 1700 en 8, 850 en 4, 425 en 2	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e47	16/15e de ton	=	213,33.. cents	divise 3200 cents en 15	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e48	15/14e de ton	=	214,28... cents	divise 3000 cents en 14	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e49	14/13e de ton	=	215,38... cents	divise 2800 cents en 13	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e50	13/12e de ton	=	216,66.. cents	divise 2600 cents en 12, 1300 en 6	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e51	12/11e de ton	=	218,18.. cents	divise 2400 cents en 11 (dbl 8ve div par 11)	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e52	11/10e de ton	=	220 cents	divise 2200 cents en 10, 1100 en 5	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp
e53	10/9e de ton	=	222,22.. cents	divise 2000 cents en 9	~ 6 div ~ 8ve	Scala tuning script .scl	Kontakt tuning script .nkp

. Il y a	5	échelles nonoctaviantes qui divisent le cycle de	la quarte (4te = 500 cents)	en 8, 7, 6, 4 et 3	(div. paires+impaires)	5/16e de ton, 5/14e de ton, 5/12e de ton, 5/8e de ton et 10/12e de ton
. Il y a	0	échelle nonoctaviante qui divise le cycle de	la quarte augmentée (4te+ = 600 cents)
. Il y a	4	échelles nonoctaviantes qui divisent le cycle de	la quinte (5te = 700 cents)	en 8, 6, 5, et 4	(div. paires+impaire)	7/16e de ton, 7/12e de ton, 7/10e de ton et 7/8e de ton
. Il y a	6	échelles nonoctaviantes qui divisent le cycle de	la sixte mineure (6te m = 800 cents)	en 15, 13, 11, 9, 7 et 5	(div. impaires)
. Il y a	3	échelles nonoctaviantes qui divisent le cycle de	la sixte majeure (6te M = 900 cents)	en 8, 7 et 5	(div. paire+impaires)
. Il y a	4	échelles nonoctaviantes qui divisent le cycle de	la septième mineure (7e m = 1000 cents)	en 13, 11, 9 et 7	(div. impaires)
. Il y a	3	échelles nonoctaviantes qui divisent le cycle de	la septième majeure (7e M 1100 cents)	en 8, 7 et 5	(div. paire+impaires)
. Il y a	3	échelles nonoctaviantes qui divisent le cycle de	l'octave et seconde mineure (8ve+2de m = 1300 cents)	en 8, 7 et 6	(div. paires+impaire)
. Il y a	3	échelles nonoctaviantes qui divisent le cycle de	l'octave et seconde majeure (8ve+2de M = 1400 cents)	en 15, 13 et 9	(div. impaires)
. Il y a	1	échelle nonoctaviante qui divise le cycle de	l'octave et tierce mineure (8ve+3ce m = 1500 cents)	en 8	(div. paire)
. Il y a	4	échelles nonoctaviantes qui divisent le cycle de	l'octave et tierce majeure (8ve+3ce M = 1600 cents)	en 15, 13, 11 et 9	(div. impaires)
. Il y a	1	échelle nonoctaviante qui divise le cycle de	l'octave et quarte (8ve+4te = 1700 cents )	en 8	(div. paire)
. Il y a	2	échelles nonoctaviantes qui divisent le cycle de	l'octave et quarte augmentée (8ve+4te+ = 1800 cents)	en 13 et 11	(div. impaires)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	l'octave et quinte (8ve+5te = 1900 cents)
. Il y a	3	échelles nonoctaviantes qui divisent le cycle de	l'octave et sixte mineure (8ve+6te m = 2000 cents)	en 13, 11 et 9	(div. impaires)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	l'octave et sixte majeure (8ve+6te M = 2100 cents)
. Il y a	3	échelles nonoctaviantes qui divisent le cycle de	l'octave et septième mineure (8ve+7e m = 2200 cents)	en 15, 13 et 12	(div. impaires+paire)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	l'octave et septième majeure (8ve+7e M = 2300 cents)
. Il y a	2	échelles nonoctaviantes qui divisent le cycle de	double octave (2.8ve = 2400 cents)	en 13 et 11	(div. impaires)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	double octave et seconde mineure (2.8ve+2de m = 2500 cents)
. Il y a	1	échelle nonoctaviante qui divise le cycle de	double octave et seconde majeure (2.8ve+2de M = 2600 cents)	en 15	(div. impaire)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	double octave et tierce mineure (2.8ve+3ce m = 2700 cents)
. Il y a	2	échelles nonoctaviantes qui divisent le cycle de	double octave et tierce majeure (2.8ve+3ce M = 2800 cents)	en 15 et 13	(div. impaires)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	double octave et quarte (2.8ve+4te = 2900 cents)
. Il y a	1	échelle nonoctaviante qui divise le cycle de	double octave et quarte augmentée (2.8ve+4te+ = 3000 cents)	en 14	(div. paire)
. Il y a	0	échelle nonoctaviante qui divise le cycle de	double octave et quinte (2.8ve+5te = 3100 cents)
. Il y a	1	échelle nonoctaviante qui divise le cycle de	double octave et sixte mineure (2.8ve+6te m = 3200 cents)	en 15	(div. impaire)

n°	nonoctaves		divisions nonoctaviantes	composition des familles
e1	1226,66..	cents	23	famille 23 : 1 enfant
e2	1230,769230......	cents	20	famille 20 : 1 enfant
e3	1187,5	cents	19	famille 19 : 1 enfant
e4	1214,285714......	cents	17	famille 17 : 2 enfants
e5	1236,36..	cents	17	famille 17 : 2 enfants
e6	1230,769230......	cents	16	famille 16 : 1 enfant
e7	1166,66..	cents	14 (ou 1250 cents pour div. 15)	famille 14 : 3 enfants (ou famille 14 : 2 enfants et famille 15 : 1 enfant qui se partage 2 familles)
e8	1225	cents	14
e9	1244,44..	cents	14
e10	1181,81..	cents	13	famille 13 : 2 enfants
e11	1213,33..	cents	13	famille 13 : 2 enfants
frontière micro et macro intervalles
e12	1173,33..	cents	11	famille 11 : 5 enfants
e13	1184,615384......	cents
e14	1222,22..	cents
e15	1237,5	cents
e16	1257,142857......	cents
e17	1166,66..	cents	10	famille 10 : 3+2 enfants avec 2 enfants qui se partagent avec la famille 9
e18	1230,769230......	cents
e19	1250	cents
e20	1272,72..	cents	10 (ou 1145,45.. cents pour div. par 9)
e21	1285,714285......	cents	10 (ou 1157,142857...... pour div. par 9)
e22	1237,5	cents	9	famille 9 : 4+2 enfants avec 2 enfants qui se partagent avec la famille 10
e23	138,461538...... (?)	cents
e24	1260	cents
e25	1142,857142......	cents
e26	1163,63..	cents	8	famille 8 : 4+1 enfants avec 1 enfant qui se partage avec la famille 7
e27	1173,33..	cents
e28	1230,769230......	cents
e29	1244,44..	cents
e30	1257,142857......	cents	8 (ou 1100 cents pour div. par 7)
e31	1120	cents	7	famille 7 : 11+1 enfants avec 1 enfant qui se partage avec la familles 6
e32	1137,5	cents
e33	1145,45..	cents
e34	1166,66..	cents
e35	1184,615384......	cents
e36	1213,33..	cents
e37	1225	cents
e38	1244,44..	cents
e39	1260	cents
e40	1272,72..	cents
e41	1283,33..	cents
e42	1292,307692......	cents	7 (ou 1107,692307...... cents pour div. par 6)
e43	1114,285714......	cents	6
e44	1120	cents
e45	1125	cents
frontière au-delà du ton
e46	1275	cents	6	famille 6 : 8+4 enfants avec 1 enfant qui se partage avec la famille 7, et 3 enfants qui se partagent avec la famille 5
e47	1280	cents
e48	1285,714285......	cents
e49	1292,307692......	cents
e50	1300	cents
e51	1309,09..	cents	6 (ou 1090,90.. cents pour div. par 5)
e52	1320	cents	6 (ou 1100 cents pour div. par 5)
e53	1333,33..	cents	6 (ou 1111,11.. cents pour div. par 5)